Shen, Chi

Jan 17 2020, New Haven, CT

不知不觉，一个quarter了，这个月好像没啥新收获，好的是论文终于开始着手了。因为一个分析选题的需要，前几天又琢磨了一下差分法，正好一道把以前的一些思考整理一下，记录下来。

最近些年，由于以计量经济学为基础的经济学实证研究的兴起，人文社科领域的定量研究也越来越火热了，写文章要是不用个双重差分都不好意思出去给人说，甚至听到过有人发出过最近某某数据快出来，又可以做双重差分了的感慨。

由于双重差分（Diff-in-Diff）的原理理解起来比较容易，分析所需要的数据也比较容易获得，再加上学术届的广泛认可，所以该方法最近些年特别的火，网上流传的教程贴也是十分丰富，一些公众号基本间隔一段时间就推送一波相关的文章用来收割一批新的订阅者。

但是，由于双重差分的原理比较简单，上手起来比较容易，很多人大部分时间都是简单的套用，没有去细琢磨差分法的一些细节问题，真正弄清楚了这些细节，才能很灵活的去衍生更多的变化。

1. Diff-in-Diff的适用场景

1.1 为什么要用双重差分

最简单的一句话就是因果识别是各个学科关注的核心问题之一，但是社会科学领域很难开展实验研究，所以需要从分析手段上想办法找到估计干预效应更准的方法。这就是为什么流行病与卫生统计学科的人不怎么热衷双重差分的原因，因为他们更关注RCT，在研究设计上就解决了随机分组的问题，直接student t或者anova就能估计出净的干预效应，通常称为average treatment effect on treated (ATT)。

1.2 什么时候可以用双重差分

简单来说就是需要进行因果识别研究的时候，具体而言通常就是政策评估时常用，因为政策评估通常为社会自然实验，无法进行随机分组和随机抽样，因此无法采用随机对照试验的方法，政策评估有四种常用方法：

• 工具变量法：寻找外生的工具变量，通过两阶段ols估计，分离出扰动项中与内生变量相关的变异，从而获得更干净的内生解释变量的效应值。具体而言就是，第一阶段用内生解释变量作为被解释变量（因变量），将工具变量作为解释变量（自变量），进行ols估计，获得内生解释变量的预测值；第二阶段则是将内生解释变量的预测值作为解释变量（自变量），将研究原本的指标作为被解释变量再进行ols估计，则内生解释变量的估计参数即为净效应值。缺点：工具变量难找
• 断点回归：本质就是趋紧局部的随机对照试验，具体介绍可见这篇帖子。
• 双重差分：通过进行两次差分获得att
• 倾向得分匹配：适用于横断面研究

双重差分分析对数据的要求，也就是什么情况下可以考虑双重差分：

• 两个时间点的个体横断面数据（微观数据）：

  两个横断面个体不是同一批人，也就是常说的两个混合截面，很多较为早期开展的survey数据是这种形式。只要能找到一个变量，能够在第一个横断面中识别出与第二个横断面中受到干预的个体相对应的个体即可，也就需要找到第一个横断面中哪些个体属于干预组。通常可以通过地区变量来分辨，对于试点政策多采取这种方法，因为追踪调查比较费时费力。缺点：无法避免两次横断面调查带来的抽样误差，因为两个横断面的个体并不是同一批人，虽然抽样误差会在组间diff的时候被减去，但这种情况需要抽样误差在对照和干预个体中是均匀分布的。

• 两期及更多期的追踪数据，本质就是面板数据：

  和上面情况一样，都是survey数据，但是为追踪调查，也就是每个时间点调查的个体都是同一批人。这种数据最优，可以进行的差分方法变化也最多，但是较难获得，好在最近些年开展的大规模人群调查都在采取追踪调查的方式。

• 两期及更多期的机构或地区数据，就是常见的机构或地区面板数据（宏观数据）：

  比第二种情况更容易获得数据，但是缺点在于很难收集到样本量足够大、分析单元足够小的数据，比如较为容易获得的省级面板数据实际缺点较大。

• 单一的横断面数据：严格来讲是无法进行双重差分设计的，但是也有采用横断面进行差分研究的实例，比如研究中国大饥荒的通过不同出生队列构建的差分模型。

1.3 双重差分的基本原理

为什么通过两次差分就能估计出净效应的原理不详述，这里只讨论一个问题：为什么RCT的研究在估计干预效应时只diff一次，而这里要diff两次？

这就涉及到了双重差分方法的一个最重要的前提假设：共同趋势（Common Trends）假设，即干预组和对照组在政策实施之前必须具有相同的发展趋势。

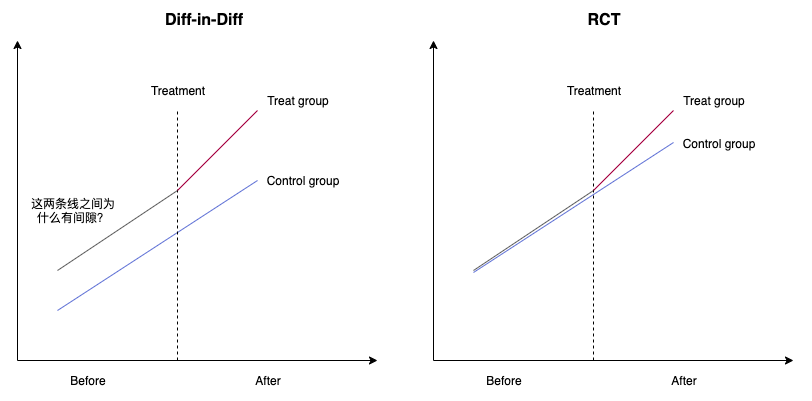
那么为什么要有这个假设呢，可以看下面的示意图：

左边的图就是最常见的双重差分原理的示意图，共同趋势假设的目的就是为了保证基线期（before）的diff，如果没有treatment，干预组和对照组之间的差异仍然是这个diff，所以在第二次差分时扣掉这个diff就能得到净干预效应。

所以这个共同趋势假设是为了保证干预和对照组在干预前后基础的变化都是一致的，它包含两层意思：一是必须趋势不变，也就是都是上升或下降或不变；二是必须平行。因此这个共同趋势假设只是一个基础，是在这个假设成立的基础上，才能推断在干预后，干预组和对照组也会（是也会，不是一定，所以这就是双重差分并不完美的地方）按照这个趋势变化，才能利用第二次差分。而有的公众号中写的是只要共同趋势满足，就可以大胆使用双重差分，其实并不是。

上面只说了共同趋势假设是为了保证反事实情况下的变化一致，但是并没有说出有这个假设的原因。应该也有人会问，为什么所有的双重差分的示意图在干预前的两条线都是平行的，但是有间隙。原因就是前面所讲的，这种自然试验无法保证干预组和对照组是随机分配的，换句话说就是这两组人在没有施加干预时，就是两个人群，所以会有差异，也就是示意的间隙。

因为这个“间隙”（就是组间差异）比较大，所以就需要在干预后把它扣除掉，如果不扣除直接对干预后的两组进行差值比较，那么这个差值中时包含了这个“间隙”的，如果这个“间隙”比真实干预效应还大，那么得到的两组差值就失去意义了，所以才会有第二次diff（第一次diff两组分别是前后减，第二次diff是在第一次的结果上干预和对照减）。

那么，如果这个“间隙”足够小呢，小到随机误差那么大，是不是就可以不用减的。那这就是为什么RCT只diff一次的原因，因为在试验设计阶段，通过严格的随机化已经保证的干预组和对照组个体的一致性，也就是已经将这个“间隙”降到足够小了，就像右边的图示意的一样。

2. Diff-in-Dff的模型设定

双重差分的基准模型如下：

\[y_{it} = \beta_1 \cdot Treat*Time + \beta_2 Treat + \beta_3 Time + \beta_0+ \epsilon_{it}\]

各参数代表意义就不解释了，其采用ols估计就行了，该模型适用于前面所提到的第一种和第二种中的两期的数据类型。

但是，如果仔细看的话，该模型就是采用的双向固定效应模型，其中treat是个体效应，time是时间效应。因此，对于多期的面板数据，你又会看见下面的模型：

\[y_{it} = \beta \cdot Treat*Time + \lambda t + \mu_i + \epsilon_{it}\]

其中没有了treat和time，取而代之是lambda和mu代表的个体效应和时间效应，因为在多期面板中，如果仍然用treat和time会过于粗糙，time只有0和1，无法识别出完整的时间效应，而treat同样存在这个问题。

当然模型还有其他变化，比如当treat为连续变量时，政策冲击不是在同一时间单一完成的，但是归根结底都是双向固定效应模型的变换形式。

3. Diff-in-Dff的变化

正如前面所将，双重差分法并不要求干预组和对照组是完全一致的，可以存在一定的差异，但是要求这种差异不随着时间产生变化，这也是在共同趋势假设成立的基础上，能够进一步推断干预后这个差异仍然是基线的差异的基础，因为前面几年是平行变化的，并不代表在政策施加之后也是平行变化的。但是这个不随时间变化的要求是无法检验的，所以这就成了双重差分法的一个无法避免的weakness。

那么，有人会问如果共同趋势不满足怎么办，当然会有其他的方法：匹配+双重差分，最常见的是psm+did，当然也可以是cem+did

对于两期的混合截面或者面板数据而言，是无法进行共同趋势检验的，所以有的论文中在这种情况下就不提共同趋势的事，对于多期面板虽然可以检验共同趋势，但是也会存在这个假设不满足的情况。

所以，为了研究的严谨性和可继续下去，有的学者就提出提出对样本进行匹配，因为共同趋势不满足的根本原因就是干预组和对照组之间差异太大，所以就通过匹配的办法让两组个体更加可比一些，将“间隙”缩小一些。

那么有的人又会问，既然前面说的横断面数据可以用匹配的方法进行效应估计，那既然都匹配了，也就是说趋近随机分组了，那么为什么还要diff两次。解释就是想要真正做到随机分组，匹配的变量需要很多，匹配的效果与RCT还是有差别，两组间的“间隙”仍然存在，所以还是需要用双重差分估计更干净的效应。

这里需要注意的一点是，应用匹配+双重差分的方法，不同的数据情况采用不同的匹配策略。

• 因为对于面板数据，得到了干预前匹配后的个体，自然就确定了干预后的个体。
• 而对于两个时点的混合截面数据，由于干预前后的个体本来就不是精确对应的，所以如果要用匹配+did的话，就需要进行三次匹配：干预前：干预 vs 对照，获得干预前匹配好的样本，然后在这个基础上，在第二期截面数据里，分别在干预组和对照组中进行 干预前 vs 干预后的匹配，这样才能严格满足要求，但是缺点是会损失较大的样本量。
• 当然，对于两个时点的混合截面数据，也可以只进行两次匹配，第一个时点：干预 vs 对照，第二个时间点：干预 vs 对照，这样做的一个前提是，要有足够的证据支持两个时点的样本都是总体的随机样本，也就是抽样误差要足够小。
• 对于psm或cem阶段，如果采取的是1:1匹配，那么在后续did回归时不需要考虑匹配权重的问题，如果采取的不是1:1匹配，则需要在回归时进行加权回归（对干预前个体匹配获得的权重，应该也要赋给干预后的）。