Chi Shen, Oct 13 2019
New Haven, CT
关于主成分分析
主成分分析(Principal component analysis)是由Pearson在1901年提出的,后来被Hotelling在1933进行了发展。
目的:
把多个相关的原始变量降维成少数几个不相关的主成分。
原理:
本质是原始变量的线性组合。
进行主成分分析的步骤
1.数据预处理
原始数据矩阵或者相关系数矩阵都可以进行分析,需要注意的几点:
- 原始数据矩阵实际是计算协方差矩阵进行的主成分分析
- 原始数据矩阵只适用于度量单位相同,或者差别不大时进行分析,如果差别大可以进行Z得分转换
- 不论是原始数据矩阵还是相关系数矩阵,都不能有缺失值
2.确定主成分个数
在计算主成分得分之前,需要先判断主成分个数,通常有四种准则:
- 根据先验经验或者理论知识
- Kaiser-Harris准则,只保留特征值大于1的主成分
- Cattell碎石检验,通过绘制特征值与主成分数的图形,只保留在图形变化最大处之上的主成分
- 平行分析,依据与初始矩阵相同大小的随机数据矩阵来判断要提取的特征值,若基于真实数据的某个特征值大于一组随机数据矩阵相 应的平均特征值,那么该主成分可以保留。
通常需要结合四种准则,综合判断主成分个数
3.计算主成分
在R语言中既可以使用base包中的princomp()函数,也可以使用psych包中的principal()函数
4.旋转主成分
旋转是一系列将成分载荷阵变得更容易解释的数学方法,它们尽可能地对成分去噪。
旋转方法有两种: + 正交旋转:使选择的成分保持不相关 + 斜交旋转:和让它们变得相关
旋转方法也会依据去噪定义的不同而不同。
最流行的正交旋转是方差极大旋转,它试图对载荷阵的列进行去噪,使得每个成分只是由一组有限的变量来解释(即载荷阵每列只有少数几个很大的载荷,其他 都是很小的载荷)。
5.解释结果并计算主成分得分
对结果进行解释,并计算各个主成分的得分,需要注意的是:
使用相关系数矩阵进行主成分分析时,无法直接获得主成分得分,只能得到原始变量的主成分系数。
主成分分析的示列
建议在R语言中,使用psych包进行主成分分析。
1.载入包和数据
示列数据集使用的是psych包中自带的Harman23.cor数据集。
library(psych)
data(Harman23.cor)
str(Harman23.cor) #可以看出Harman23.cor是一个list,需要提取出分析使用的cov数据集
## List of 3
## $ cov : num [1:8, 1:8] 1 0.846 0.805 0.859 0.473 0.398 0.301 0.382 0.846 1 ...
## ..- attr(*, "dimnames")=List of 2
## .. ..$ : chr [1:8] "height" "arm.span" "forearm" "lower.leg" ...
## .. ..$ : chr [1:8] "height" "arm.span" "forearm" "lower.leg" ...
## $ center: num [1:8] 0 0 0 0 0 0 0 0
## $ n.obs : num 305
df <- Harman23.cor$cov
str(df)
## num [1:8, 1:8] 1 0.846 0.805 0.859 0.473 0.398 0.301 0.382 0.846 1 ...
## - attr(*, "dimnames")=List of 2
## ..$ : chr [1:8] "height" "arm.span" "forearm" "lower.leg" ...
## ..$ : chr [1:8] "height" "arm.span" "forearm" "lower.leg" ...
2.判断主成分个数
psych包中给出了一个特别有用的函数fa.parallel(),可以很方便的同时给出Kaiser-Harris准则,Cattell碎石检验,平行分析的结果。
由上步骤可以看出,df实际为相关系数矩阵,n.obs是指定原始观测数,n.iter是指定平行分析的随机迭代次数,fa是用来指定进行主成分分析, 取值有三类(‘fa’,‘pc’,‘both’)。
由结果看出,特征值大于1,拐点之上,大于随机的特征值,满足以上三个条件,只有前两个主成分,因此主成分个数为2.
fa.parallel(df, n.obs = 302, n.iter = 100, main = "Parallel Analysis Scree Plots", fa = 'pc', show.legend = TRUE)
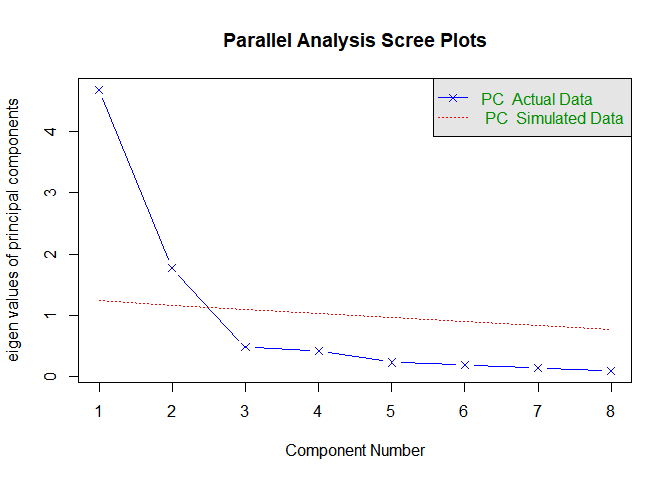
## Parallel analysis suggests that the number of factors = NA and the number of components = 2
3.主成分分析
结果中
- PC1和PC2既为2个主成分在各个原始变量上的载荷(loading,也就是相关系数),可以看出系数都较高
- h2为成分公因子方差,用来说明主成分对每个变量的方差解释度,此值越高说明解释力度越大
- u2栏指成分唯一性——方差,用来说明无法被主成分解释的比例,h2与u2之和为1
- Proportion Var为每个主成分对整个数据集的解释程度
- Cumulative Var是Proportion Var的累计和,其值至少应该需大于0.80以上
可以看出,PC1和PC2在部分变量上都有较高的解释度,不满足各个主成分之间应该正交的条件,需进行旋转
principal(df, nfactors = 2, rotate = 'none', n.obs = 302, scores = TRUE)
## Principal Components Analysis
## Call: principal(r = df, nfactors = 2, rotate = "none", n.obs = 302,
## scores = TRUE)
## Standardized loadings (pattern matrix) based upon correlation matrix
## PC1 PC2 h2 u2 com
## height 0.86 -0.37 0.88 0.123 1.4
## arm.span 0.84 -0.44 0.90 0.097 1.5
## forearm 0.81 -0.46 0.87 0.128 1.6
## lower.leg 0.84 -0.40 0.86 0.139 1.4
## weight 0.76 0.52 0.85 0.150 1.8
## bitro.diameter 0.67 0.53 0.74 0.261 1.9
## chest.girth 0.62 0.58 0.72 0.283 2.0
## chest.width 0.67 0.42 0.62 0.375 1.7
##
## PC1 PC2
## SS loadings 4.67 1.77
## Proportion Var 0.58 0.22
## Cumulative Var 0.58 0.81
## Proportion Explained 0.73 0.27
## Cumulative Proportion 0.73 1.00
##
## Mean item complexity = 1.7
## Test of the hypothesis that 2 components are sufficient.
##
## The root mean square of the residuals (RMSR) is 0.05
## with the empirical chi square 46.77 with prob < 1.1e-05
##
## Fit based upon off diagonal values = 0.99
4.主成分分析
从结果可以看出,PC1和PC2变成了RC1和RC2,即表示经过旋转了,可以很清楚的看出:
旋转后,RC1在前4个变量(height – lower.leg)上具有更高的解释度
RC2在后4个变量(weight – chest.width)上具有更高的解释度
说明两个主成分正交(不相关)
同时可以发现,旋转后并不改变Cumulative Var
dfp <- principal(df, nfactors = 2, rotate = 'varimax', n.obs = 302, scores = TRUE)
dfp
## Principal Components Analysis
## Call: principal(r = df, nfactors = 2, rotate = "varimax", n.obs = 302,
## scores = TRUE)
## Standardized loadings (pattern matrix) based upon correlation matrix
## RC1 RC2 h2 u2 com
## height 0.90 0.25 0.88 0.123 1.2
## arm.span 0.93 0.19 0.90 0.097 1.1
## forearm 0.92 0.16 0.87 0.128 1.1
## lower.leg 0.90 0.22 0.86 0.139 1.1
## weight 0.26 0.88 0.85 0.150 1.2
## bitro.diameter 0.19 0.84 0.74 0.261 1.1
## chest.girth 0.11 0.84 0.72 0.283 1.0
## chest.width 0.26 0.75 0.62 0.375 1.2
##
## RC1 RC2
## SS loadings 3.52 2.92
## Proportion Var 0.44 0.37
## Cumulative Var 0.44 0.81
## Proportion Explained 0.55 0.45
## Cumulative Proportion 0.55 1.00
##
## Mean item complexity = 1.1
## Test of the hypothesis that 2 components are sufficient.
##
## The root mean square of the residuals (RMSR) is 0.05
## with the empirical chi square 46.77 with prob < 1.1e-05
##
## Fit based upon off diagonal values = 0.99
5.计算主成分得分
在principal函数中的scores即是制定是否计算主成分得分的,如果为TRUE,则在dfp中已保存有得分,利用dfp$scores即可以取出得分。
但是本示列中使用的是相关系数矩阵,无法计算得分,只能计算得分权重,为:
dfp$weights
## RC1 RC2
## height 0.27524417 -0.04748169
## arm.span 0.29673051 -0.08005490
## forearm 0.29823990 -0.09158460
## lower.leg 0.28014088 -0.06027214
## weight -0.06053059 0.33228637
## bitro.diameter -0.07752349 0.32477593
## chest.girth -0.10366026 0.33763942
## chest.width -0.03730720 0.27392667