flowchart LR
A[概览] --> B(异常值识别处理)
B --> C{缺失值识别与处理}
C --> D[重复值识别与处理]
D --> E[标准化变量和取值]
3 数据的清洗
3.1 引子
正如前文所述,数据清洗(Data Cleaning)和数据准备(Data Preparation)工作通常会占掉整个数据分析过程70%到80%的时间,这一点基本被很多学者所认可,因此,应该清楚地认识到数据清洗工作的重要性。然而,很多学者,特别是还处在科研早期阶段的硕博士研究生,十分热衷于跑模型(Run model)。拿到数据既不详细摸索数据结构,也不观察变量分布情况,简单地描述一下数据后,就开始跑各种回归,目的只在发现统计显著的回归系数。这是一个不太好的研究习惯。
3.2 数据清洗相关概念
3.2.1 数据清洗(Data Cleaning)
何谓数据清洗?目前其实没有统一的定义,但是在不同的学科领域中,数据清洗的目标和内容基本是明确一致的,那就是识别、修改或删除不正确和不完整的数据,识别和删除重复信息和无关数据,以及按一定的标准统一数据格式、缺失值和拼写错误,规范数据结构,从而更好地为下一步分析工作服务。结合Microsoft、Amazon以及 (Ron, 2008) 的观点,本书将常见的数据清洗步骤归纳如下:
- 识别并处理异常值:异常值会对数据分布产生明显影响,干扰正常结果,并显著影响模型性能,通常进行删除。
- 识别并处理缺失数据:缺失值是无法避免的问题,但需要掌握数据中的缺失特征并予以处理。
- 识别并处理重复数据:删除重复信息。
- 规范变量类型及取值:根据变量的属性特征,正确将其存储为数值、字符、日期、时间等类型,并统一取值类型。
- 识别并处理不相关数据:确定特定分析的关键字段并从分析中删除不相关数据。
- 识别并处理结构错误:识别数据库在录入和建立过程中出现的错误,如输入错误、错行等。
3.2.2 整洁数据(Tidy Data)
整洁数据(Tidy Data)是由Posit公司(之前名称为Rstudio)的首席科学家Hadley Wickham提出的,初衷是为了简化数据清洗的流程,提高数据清洗效率。Wickham (2014) 认为Tidy Data更易于操作、建模和可视化,并且应该具备三种特征:
- Each variable is a column, and that column contains one “type” of data.
- Each observation is a row.
- Each type of observational unit is a table.
打眼一看,你可能觉得上面三句话说的是废话,心里想着大家不是都是这么建数据库的吗?其实不然,比如可以看下面的例子。
如 表 3.1 是日常工作和研究中非常常见的建数据库方式,但是这样的方式对于统计分析来说并不友好。比如当你想要知道每一科考试得分的最大值最小值时,你通常需要对数学、语文、英语重复三次同样的操作。
| 姓名 | 数学 | 语文 | 英语 |
|---|---|---|---|
| 张三 | 80 | 90 | 95 |
| 李四 | 88 | 95 | 97 |
再比如,当有多次考试的成绩需要记录时,很多人会选择 表 3.2 这样的方式,但是这样的结构在数据分析时会更不友好。
| 姓名 | 第一次 | 第二次 | ||||
|---|---|---|---|---|---|---|
| 数学 | 语文 | 英语 | 数学 | 语文 | 英语 | |
| 张三 | 80 | 90 | 95 | 85 | 92 | 97 |
| 李四 | 88 | 95 | 97 | 87 | 90 | 98 |
符合Tidy Data要求的建立数据库方式应该如 表 3.3 所示,在这种结构下,结合Group by等操作,会给数据分析带来很大的便利。
| 姓名 | 考试 | 学科 | 得分 |
|---|---|---|---|
| 张三 | 第一次模拟考 | 数学 | 80 |
| 李四 | 第一次模拟考 | 数学 | 88 |
| 张三 | 第一次模拟考 | 语文 | 90 |
| 李四 | 第一次模拟考 | 语文 | 95 |
| 张三 | 第一次模拟考 | 英语 | 95 |
| 李四 | 第一次模拟考 | 英语 | 97 |
| 张三 | 第二次模拟考 | 数学 | 85 |
| 李四 | 第二次模拟考 | 数学 | 87 |
| 张三 | 第二次模拟考 | 语文 | 92 |
| 李四 | 第二次模拟考 | 语文 | 90 |
| 张三 | 第二次模拟考 | 英语 | 97 |
| 李四 | 第二次模拟考 | 英语 | 98 |
关于Tidy Data的内容还有很多,具体可以详细参考 Wickham (2014) 的文章,这里就不进行搬运工作了。在设计数据库的时候,只需要记住不要把数据展示形式当成数据库的结构形式就可以。
3.3 数据清洗内容
一般情况下,数据清洗可以按照 图 3.1 所示流程进行。由于异常值处理、重复值处理、规范变量类型及取值、识别并处理结构错误的内容相对比较简单,在本节中仅通过简单举例说明。而缺失值的处理流程相对复杂,则进行了详细说明。
3.3.1 数据概览
数据清洗的第一步就是需要对数据库有一个整体的把握,如有多少个变量、多少条记录、变量类型如何、取值是什么等。在规范的研究项目(如注册的药物/器械临床试验)中,这些信息会记录在Codebook中随同数据一并交给统计师,通过翻阅Codebook就可以清楚地了解以上这些信息。这就是为何本书在 小节 3.3.3 中强调整理和制作Codebook的重要性。然而,很多时候,对于大部分的问卷调查数据而言,很少见到有研究者严格按照类似临床试验的要求建立和管理数据库的,以及对于从医院、互联网平台等处获取的数据而言,都不会事先提供这些信息,因此拿到数据库的第一步就是去了解这些信息。
一般我将这一步称为数据库的概览(Overview),在R中通常使用str()函数或者glimpse()函数可以大致对数据结构有一个初步了解,更为推荐的工具和方法可参见 小节 4.2.2 ,本节仅给出简单的示例,具体如下:
data(mtcars)
dplyr::glimpse(mtcars[1:5, 1:6])Rows: 5
Columns: 6
$ mpg <dbl> 21.0, 21.0, 22.8, 21.4, 18.7
$ cyl <dbl> 6, 6, 4, 6, 8
$ disp <dbl> 160, 160, 108, 258, 360
$ hp <dbl> 110, 110, 93, 110, 175
$ drat <dbl> 3.90, 3.90, 3.85, 3.08, 3.15
$ wt <dbl> 2.620, 2.875, 2.320, 3.215, 3.4403.3.2 规范变量类型及取值
严格来说,这一步工作属于数据库管理的内容范畴,不应该在数据清洗阶段。但是,考虑到现在的研究,很多时候拿到的就是非常自然和原始的数据,这些工作也需要在数据清洗的时候进行。规范变量类型和取值的具体含义是指,数值型变量在数据库中的类型应该为Int或者Float,如年龄或者收入等指标;字符变量在数据库应该为String,如家庭住址或者出院诊断等指标;日期就应该Date,时间就应该是Time;另有一类较为特殊的是分类变量,如性别或学历等,可以用0、1、2等数字编码后,以Int类型存储,亦可直接以String类型存储为“男”和“女”等,两种方法各有利弊,根据研究习惯选择即可。
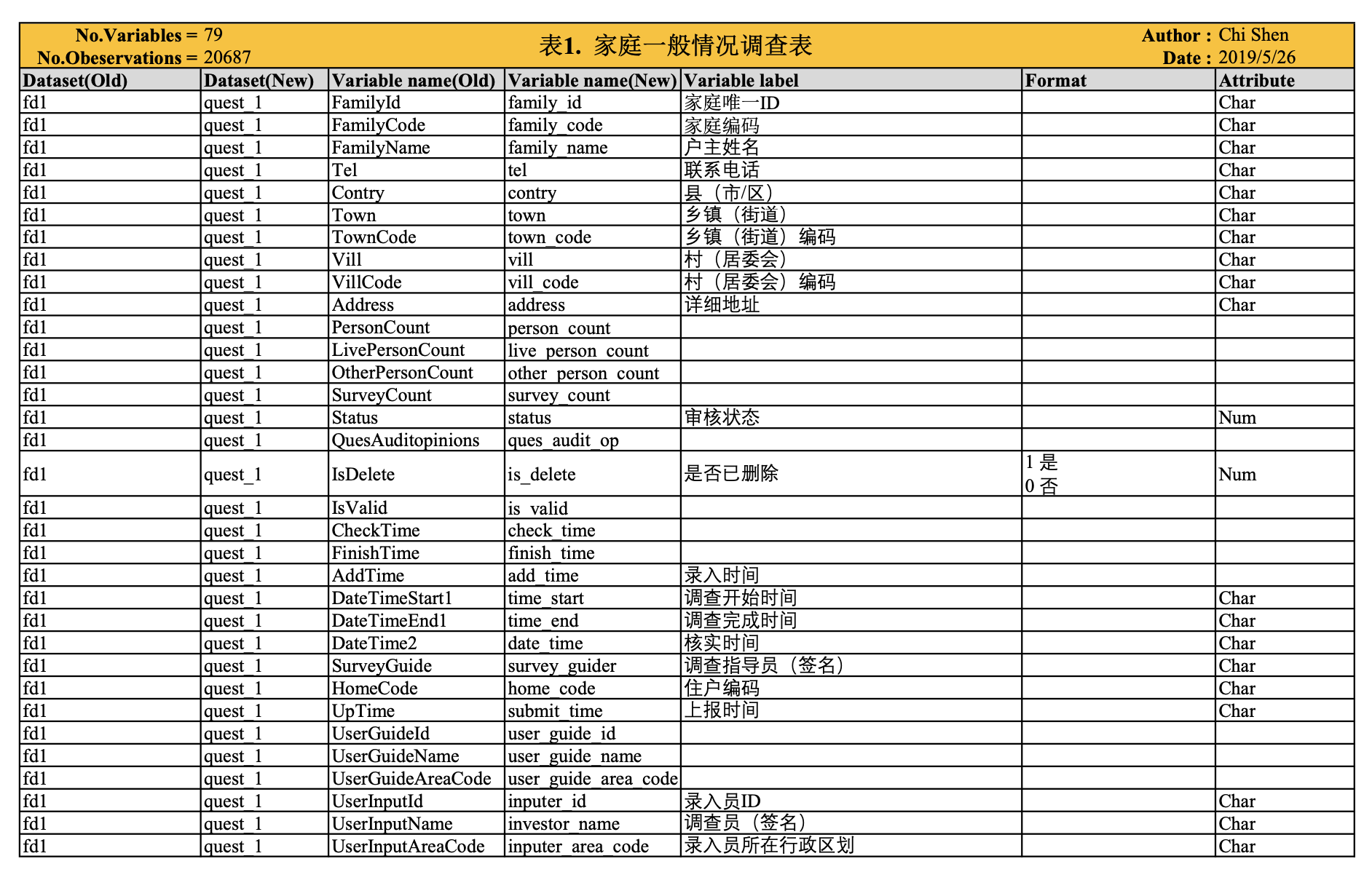
3.3.3 数据字典
数据字典(Data dictionary)也称作Codebook或者Specification,是指详细记录数据库中的变量名、变量内容、变量取值、变量标签、变量属性等信息,其作用主要是为了方便统计分析过程中检查和查看变量。
数据字典可以手动整理,也可以通过统计软件中的函数生成,如Stata中的codebook命令,R中也有codebookr和datadictionary两个package。
下面给出一个我之前整理的codebook示例,如 图 3.2 和 图 3.3

3.3.4 异常值(Outliers)处理
异常值处理根据变量的类型不同采取的方法有所区别。对于数值型变量1 采用直方图(Histogram)、箱式图(Boxplot)或者小提琴图(Violin plot)可直观的了解异常值的分布情况;对于分类变量采用频数频率表或交叉表(Crosstable)可清晰地了解异常值情况。关于作图和作表方法可详见本书后续章节 。
关于数值型变量异常值的判定标准,大致可以分为以下三种方法:
- 分位数法:通过计算1%和99%处的分位数,并将其作为上下界,界限之外的即为异常值。
- 四分位数间距法:通过计算25%和75%的分位数,也就是四分位数Q1和Q3,以及其间距IQR,然后计算异常值的上下限分别为:Q1 - 1.5 x IQR和Q3 + 1.5 x IQR。
- 标准差法:将数据均值加减3~5个标准差,定义为上下界。
关于数值型变量异常值的处理,如果是问卷数据,通常需要首先核对原始数据,排除因录入错误导致的数据异常,若排除此种原因,可采取截尾方法,剔除异常值。
3.4 缺失值(Missing Value)处理
由于这部分内容较多,因此单独用一节来介绍,本部分主要参考 (高涛 等, 2013; Kabacoff, 2013; van Buuren 等, 2011)。Missing Value的处理也是非常重要的一个环节,因此规范的缺失数据的处理直接影响着研究结果的稳健性和真实性,也是研究能够Reproductive的重要保障。通常,处理缺失值的步骤如下:
- 识别缺失数据。
- 检查导致数据缺失的原因。
- 删除包含缺失值的实例或是合理的数值代替(插补)缺失值。
3.4.1 识别缺失数据
3.4.1.1 缺失数据分类
在识别缺失数据之前,先来了解一下缺失数据的分类,它直接关系到处理缺失值方式的选择。
- 完全随机缺失。若某变量的缺失数据与其他任何观测或未观测变量都不相关,则数据为完全随机缺失(MCAR)。注意,如果每个有缺失值的变量都是MCAR,那么可以将数据完整的实例看做是对更大数据集的一个简单随机抽样。
- 随机缺失 若某变量上的缺失数据与其他观测变量相关,与它自己的未观测值不相关,则数据为随机缺失(MAR)。
- 非随机缺失 若缺失数据不属于MCAR或MAR,则数据为非随机缺失(NMAR)。
例如:
- (1)在最近一个问卷调查中,发现一些项常常一同缺失。很明显这些项聚集在一起,因为调查对象没有意识到问卷的第三页的背面也包含了这些项目。此时,可以认为这些数据是MCAR。
- (2)在一个关于全球领导风格的调查中,学历变量经常性地缺失。调查显示欧洲的调查对象更可能在此项目上留白,这说明某些特定国家的调查对象没有理解变量的分类。此时,这种数据最可能是MAR。
大部分处理缺失数据的方法都假定数据是MCAR或MAR。此时,你可以忽略缺失数据的生成机制。当数据是NMAR时,想对它进行恰当地分析比较困难,既要对感兴趣的关系进行建模,还要对缺失值的生成机制进行建模。
3.4.1.2 识别缺失值
此次只用R来演示软件操作过程,Stata及SAS等其他软件可自行查阅相关文档。以下研究主要使用R的VIM包,以及该包中自带的sleep数据集进行演示。
sleep数据集简介
睡眠变量包含睡眠中做梦时长(Dream)、不做梦的时长(NonD)以及它们的和(Sleep)。体质变量包含体重(BodyWgt,单位为千克)、脑重(BrainWgt,单位为克)、寿命(Span,单位为年)和妊娠期(Gest,单位为天)。生态学变量包含物种被捕食的程度(Pred)、睡眠时暴露的程度(Exp)和面临的总危险度(Danger)。
1) 简单探索
通常,R中使用is.na()函数来判断变量是否包含缺失值,其函数返回对象为一个逻辑向量,可以作为一种十分方便的识别缺失值的快捷方法。但是is.na()函数每次仅只能判断一个变量是否包含缺失值,当需要快速对较多变量进行判断时,需要结合apply()族函数来提高效率,具体如以下代码,即可实现对数据集中所有变量的缺失值数量进行统计。
library(magrittr)
library(knitr)
missing <- function(df) {
chk_miss <- df[, lapply(.SD, function(x){sum(is.na(x))}),
.SDcols = names(df)] %>%
transpose(keep.names = "varname")
return(chk_miss[chk_miss$V1 >0, ])
}
missing(df) %>% kable()此外,也可使用VIM包中的complete.cases()函数。该函数可以识别数据框(data.frame)每一行是否包含有缺失值,若某一行的所有变量(列) 均不包含缺失值,则返回TRUE,反之则返回FALSE。那么,complete.cases()函数回返回一个与原始数据框行数相等的逻辑向量,利用其返回对象结合切片操作,则可实现对缺失情况的筛选。此操作也可以使用na.omit()函数实现。
library(VIM)
data(sleep, package = "VIM")
# 筛选出不含任一缺失值的行
sleep[complete.cases(sleep[, 1:5]), 1:5] BodyWgt BrainWgt NonD Dream Sleep
2 1.000 6.60 6.3 2.0 8.3
5 2547.000 4603.00 2.1 1.8 3.9
6 10.550 179.50 9.1 0.7 9.8
7 0.023 0.30 15.8 3.9 19.7
8 160.000 169.00 5.2 1.0 6.2
9 3.300 25.60 10.9 3.6 14.5
10 52.160 440.00 8.3 1.4 9.7
11 0.425 6.40 11.0 1.5 12.5
12 465.000 423.00 3.2 0.7 3.9
13 0.550 2.40 7.6 2.7 10.3
15 0.075 1.20 6.3 2.1 8.4
16 3.000 25.00 8.6 0.0 8.6
17 0.785 3.50 6.6 4.1 10.7
18 0.200 5.00 9.5 1.2 10.7
19 1.410 17.50 4.8 1.3 6.1
20 60.000 81.00 12.0 6.1 18.1
22 27.660 115.00 3.3 0.5 3.8
23 0.120 1.00 11.0 3.4 14.4
25 85.000 325.00 4.7 1.5 6.2
27 0.101 4.00 10.4 3.4 13.8
28 1.040 5.50 7.4 0.8 8.2
29 521.000 655.00 2.1 0.8 2.9
32 0.005 0.14 7.7 1.4 9.1
33 0.010 0.25 17.9 2.0 19.9
34 62.000 1320.00 6.1 1.9 8.0
35 0.122 3.00 8.2 2.4 10.6
36 1.350 8.10 8.4 2.8 11.2
37 0.023 0.40 11.9 1.3 13.2
38 0.048 0.33 10.8 2.0 12.8
39 1.700 6.30 13.8 5.6 19.4
40 3.500 10.80 14.3 3.1 17.4
42 0.480 15.50 15.2 1.8 17.0
43 10.000 115.00 10.0 0.9 10.9
44 1.620 11.40 11.9 1.8 13.7
45 192.000 180.00 6.5 1.9 8.4
46 2.500 12.10 7.5 0.9 8.4
48 0.280 1.90 10.6 2.6 13.2
49 4.235 50.40 7.4 2.4 9.8
50 6.800 179.00 8.4 1.2 9.6
51 0.750 12.30 5.7 0.9 6.6
52 3.600 21.00 4.9 0.5 5.4
54 55.500 175.00 3.2 0.6 3.8
56 0.060 1.00 8.1 2.2 10.3
57 0.900 2.60 11.0 2.3 13.3
58 2.000 12.30 4.9 0.5 5.4
59 0.104 2.50 13.2 2.6 15.8
60 4.190 58.00 9.7 0.6 10.3
61 3.500 3.90 12.8 6.6 19.4# 或
na.omit(sleep[, 1:5]) BodyWgt BrainWgt NonD Dream Sleep
2 1.000 6.60 6.3 2.0 8.3
5 2547.000 4603.00 2.1 1.8 3.9
6 10.550 179.50 9.1 0.7 9.8
7 0.023 0.30 15.8 3.9 19.7
8 160.000 169.00 5.2 1.0 6.2
9 3.300 25.60 10.9 3.6 14.5
10 52.160 440.00 8.3 1.4 9.7
11 0.425 6.40 11.0 1.5 12.5
12 465.000 423.00 3.2 0.7 3.9
13 0.550 2.40 7.6 2.7 10.3
15 0.075 1.20 6.3 2.1 8.4
16 3.000 25.00 8.6 0.0 8.6
17 0.785 3.50 6.6 4.1 10.7
18 0.200 5.00 9.5 1.2 10.7
19 1.410 17.50 4.8 1.3 6.1
20 60.000 81.00 12.0 6.1 18.1
22 27.660 115.00 3.3 0.5 3.8
23 0.120 1.00 11.0 3.4 14.4
25 85.000 325.00 4.7 1.5 6.2
27 0.101 4.00 10.4 3.4 13.8
28 1.040 5.50 7.4 0.8 8.2
29 521.000 655.00 2.1 0.8 2.9
32 0.005 0.14 7.7 1.4 9.1
33 0.010 0.25 17.9 2.0 19.9
34 62.000 1320.00 6.1 1.9 8.0
35 0.122 3.00 8.2 2.4 10.6
36 1.350 8.10 8.4 2.8 11.2
37 0.023 0.40 11.9 1.3 13.2
38 0.048 0.33 10.8 2.0 12.8
39 1.700 6.30 13.8 5.6 19.4
40 3.500 10.80 14.3 3.1 17.4
42 0.480 15.50 15.2 1.8 17.0
43 10.000 115.00 10.0 0.9 10.9
44 1.620 11.40 11.9 1.8 13.7
45 192.000 180.00 6.5 1.9 8.4
46 2.500 12.10 7.5 0.9 8.4
48 0.280 1.90 10.6 2.6 13.2
49 4.235 50.40 7.4 2.4 9.8
50 6.800 179.00 8.4 1.2 9.6
51 0.750 12.30 5.7 0.9 6.6
52 3.600 21.00 4.9 0.5 5.4
54 55.500 175.00 3.2 0.6 3.8
56 0.060 1.00 8.1 2.2 10.3
57 0.900 2.60 11.0 2.3 13.3
58 2.000 12.30 4.9 0.5 5.4
59 0.104 2.50 13.2 2.6 15.8
60 4.190 58.00 9.7 0.6 10.3
61 3.500 3.90 12.8 6.6 19.4#筛选出含有一个或多个缺失值的行
sleep[!complete.cases(sleep[, 1:5]), 1:5] BodyWgt BrainWgt NonD Dream Sleep
1 6654.000 5712.0 NA NA 3.3
3 3.385 44.5 NA NA 12.5
4 0.920 5.7 NA NA 16.5
14 187.100 419.0 NA NA 3.1
21 529.000 680.0 NA 0.3 NA
24 207.000 406.0 NA NA 12.0
26 36.330 119.5 NA NA 13.0
30 100.000 157.0 NA NA 10.8
31 35.000 56.0 NA NA NA
41 250.000 490.0 NA 1.0 NA
47 4.288 39.2 NA NA 12.5
53 14.830 98.2 NA NA 2.6
55 1.400 12.5 NA NA 11.0
62 4.050 17.0 NA NA NA从结果可以看出,完整数据集中有62条观测值,其中BodyWgt等5个变量不含缺失值的观测只有48条,14条含一个或多个缺失值。由于逻辑值TRUE和FALSE分别等价于数值1和0,使用is.na()函数,联合sum()和mean()函数来获取关于缺失数据的有用信息。如:
sum(is.na(sleep$Dream))[1] 12mean(is.na(sleep$Dream))[1] 0.1935484mean(!complete.cases(sleep))[1] 0.3225806结果表明变量Dream有12个缺失值,19.35%的实例在此变量上有缺失值。另外,数据集中32.26%的实例包含一个或多个缺失值。另外一种方法是,采用mice包中的md.pattern()函数来生成缺失值矩阵,如下:
library(mice)
md.pattern(sleep[, 1:5], plot = FALSE)以上代码输出结果为一个矩阵(matrix),其中,最右侧列显示的是含缺失值变量数,最左侧列显示符合条件的观测数,其他列中的0和1为指示值,0变量缺失,1表示无缺失。例如,第一行结果表示所选择的BodyWgt等5个变量均无缺失的观测有48条,此结果与complete.cases()函数得出结果一致;第二行结果表示Dream和NonD同时缺失,其他三个变量不缺失的观测有10条。那么,sleep数据集中BodyWgt等5个变量中20条含有缺失值的观测,一共包含缺失值(48 × 0) + (10 × 2) + (2 × 2) + (2 × 3) = 30个。
2) 以图形探索缺失数据
虽然表格的输出也很简洁,但是图形的输出会更直观,此时可以采用VIM包中的aggr()和matrixplot()函数。
aggr(sleep,
prop = FALSE,
col = c("grey", "orange", "red"),
combined = FALSE,
numbers = TRUE,
labels = TRUE)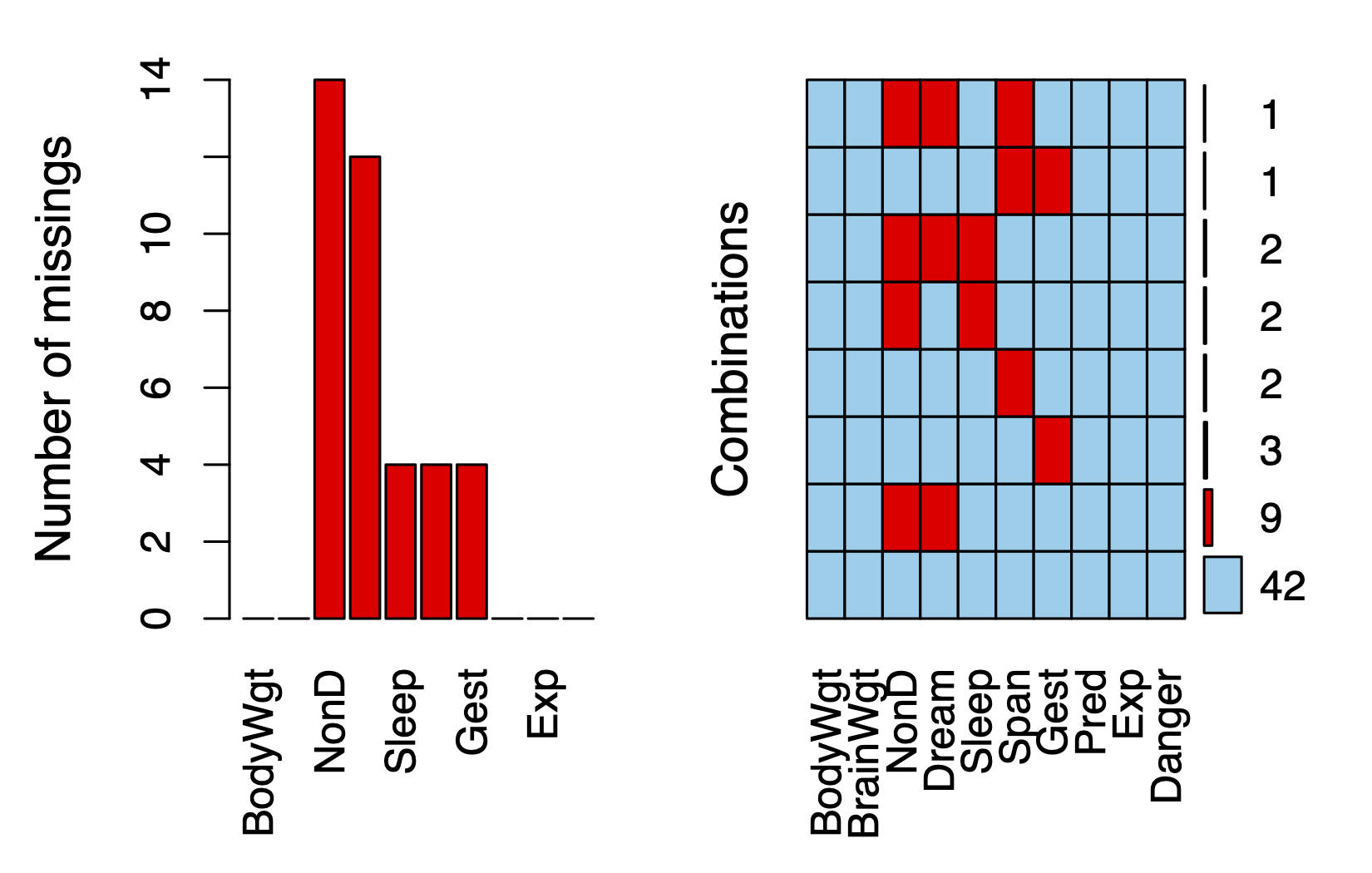
如 图 3.4, 左侧的红色条图分别显示了所有variable的缺失值数量,可以清楚的看出Gest变量有4个缺失值等。右侧的图中,红色代表缺失,可以看出无任何缺失的observation共有42条,同时了缺失NonD和Dream的observation共有9条。
matrixplot(sleep)
Click in a column to sort by the corresponding variable.
To regain use of the VIM GUI and the R console, click outside the plot region.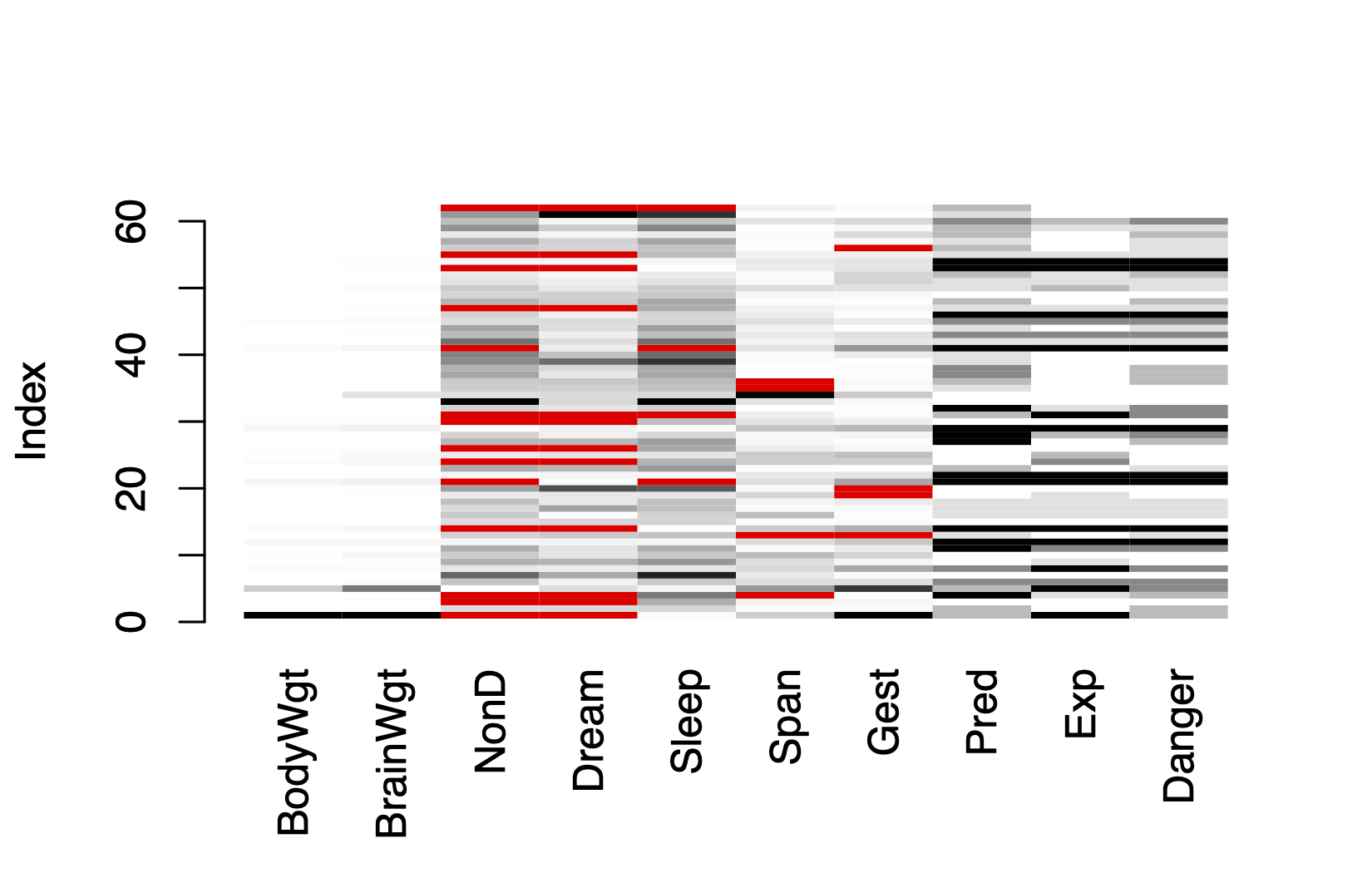
matrixplot()函数可生成展示每个实例数据的图形。此处,数值型数据被重新转换到[0, 1]区间,并用灰度来表示大小:浅色表示值小,深色表示值大。默认缺失值为红色。 图 3.5, 横轴展示了全部的variable,纵轴显示了全部observation,从图中可以清楚的了解缺失值的分布情况,默认是按照第一个变量BodyWgt从小到大排序过。
3.4.2 探索缺失原因或模式
3.4.2.1 通过图形捕捉缺失原因或模式
通过@fig-miss-2 的矩阵图中,可以看出某些变量的缺失值模式是否与其他变量的真实值有关联。此图中可以看到,无缺失值的睡眠变量(Dream、NonD和Sleep)对应着较小的体重(BodyWgt)或脑重(BrainWgt)。此时,可以采用VIM包中的marginplot()函数和ggstatsplot包中的ggscatterstats()函数可生成一幅散点图,函数可生成一幅散点图,并观察变量之间的关系,具体代码如下。
marginplot(sleep[c("Dream", "Sleep")],
col = c("darkgrey", "orange", "red"),
pch = c(20))
library(ggstatsplot)
ggscatterstats(
data = sleep,
x = Dream,
y = Sleep,
xlab = "Dream",
ylab = "Sleep"
)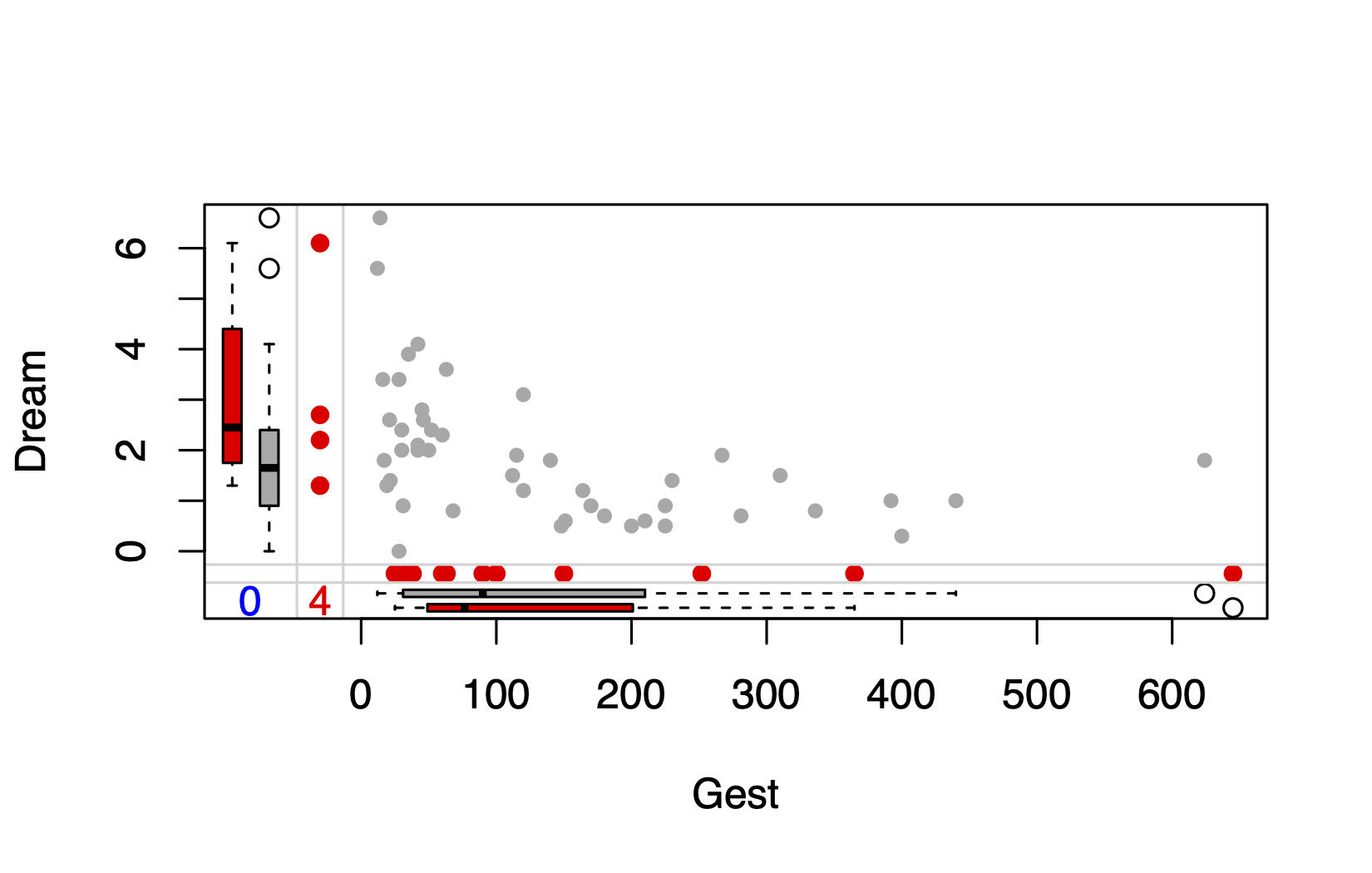
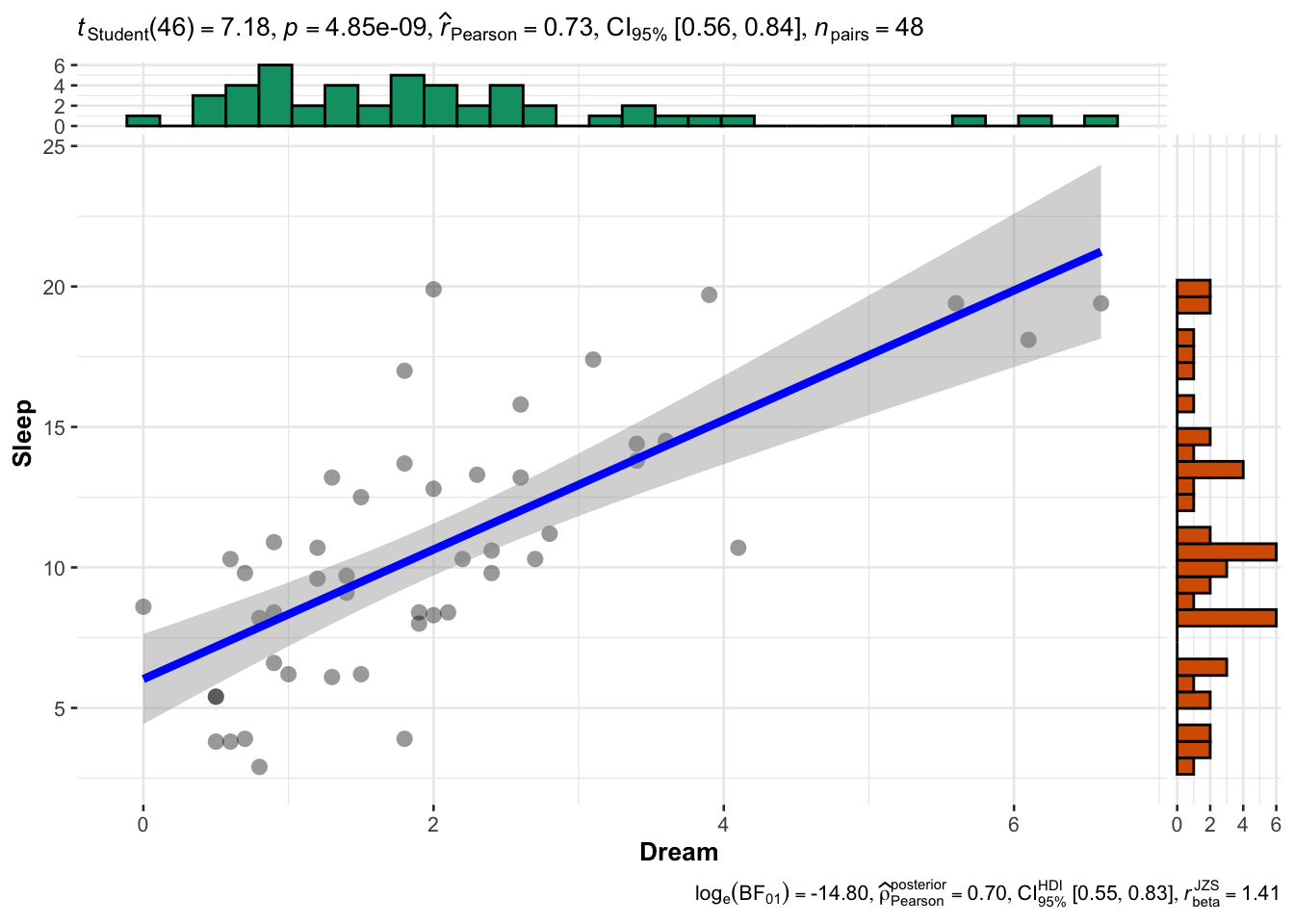
图 3.6 共显示了两部分信息,(a)散点图(b)边界显示缺失信息,具体为:
• 横轴为Dream变量,边界的箱式图显示的是Dream变量在Sleep变量缺失和非缺失状态下的分布情况,其中橙色表示Sleep变量缺失值,灰色代表Sleep变量非缺失值。 • 纵轴为Sleep变量,边界的箱式图显示的是Sleep变量在Dream变量缺失和非缺失状态下的分布情况,其中橙色表示Dream变量缺失值,灰色代表Dream变量非缺失值。 • 灰色散点为Dream与Sleep的散点图。 • 左下角的红色数字表示Dream与Sleep共同缺失的观测数量。
从结果可以看出,Dream与Sleep成正相关关系,且当Sleep变量为缺失值时,对应更小的Dream值。
3.4.2.2 通过相关性探索缺失值
图形展示了缺失变量之间可能的相关关系,进一步可用指示变量替代数据集中的数据(1表示缺失,0表示存在),这样生成的矩阵有时称作影子矩阵。求这些指示变量间和它们与初始(可观测)变量间的相关性,有助于观察哪些变量常一起缺失,以及分析变量“缺失”与其他变量间的关系。具体如下:
# 管道函数包
library(magrittr)
# 将是否缺失的逻辑变量转换为0和1变量的数据框形式
a <- abs(is.na(sleep)) %>%
as.data.frame()
b <- apply(a, 2, sum) %>%
.[which(. != 0)] %>%
names()
# 提取出缺失数据
c <- subset(a, select = b)
# 对缺失数据进行相关分析
cor(c, y = NULL) NonD Dream Sleep Span Gest
NonD 1.00000000 0.90711474 0.48626454 0.01519577 -0.14182716
Dream 0.90711474 1.00000000 0.20370138 0.03752394 -0.12865350
Sleep 0.48626454 0.20370138 1.00000000 -0.06896552 -0.06896552
Span 0.01519577 0.03752394 -0.06896552 1.00000000 0.19827586
Gest -0.14182716 -0.12865350 -0.06896552 0.19827586 1.00000000指示变量相关系数矩阵如表3-7所示,可以看出Dream变量常常与NonD变量一起缺失(r = 0.91),而Sleep变量和Dream变量之间缺失发生的关联性可能不大(r = 0.20)。
3.4.3 缺失值的处理
在对缺失数据进行识别和探索后,下一步就是对缺失数据进行填补,但是在进行下一步之前,需要前面的工作弄清楚几个问题,以便选择合理的缺失值处理方式:
- 缺失数据的比例为多少。
- 哪些变量上存在缺失,是否存在某种明显的分布趋势。
- 缺失的类型,完全随机(MCAR)、随机(MAR)或非随机(NMAR)。
3.4.3.1 缺失值处理方式
缺失值的处理通常有以下4种方法,其中前三种处理方式比较常用。除非特别必要,一般情况下较少会选择填补法。另外需要强调的是,若采取删除缺失值的处理方式,通常需要对删除缺失前的数据库和删除后的数据库进行比较,主要采用描述性统计方法检验关键的人口学特征是否存在差异。若不存在差异方可说明采用删除缺失值的方式是可取的,否则就会改变样本的代表性。
不予处理:如果有一小部分数据(如小于10%)随机分布在整个数据集中(MCAR),那么你可以分析数据完整的实例,这样仍可以得到可靠且有效的结果。
删除变量(列):如果缺失数据集中在几个相对不太重要的变量上,那么你可以删除这些变量,然后再进行正常的数据分析.
删除观测(行):在完整的数据分析中,只有每个变量都包含了有效数据值的观测才会保留下来做进一步的分析。实际上,这样会导致包含一个或多个缺失值的任意一行都会被删除,这种处理方法被称为行删除法(listwise)、个案删除(casewise)或剔除。大部分流行的统计软件包都默认采用行删除法来处理缺失值。例如,在Stata或者SAS中,进行交叉表(Crosstable)、t检验(Ttest)、方差检验(Anova)或者回归(Regression)分析时,默认为自动剔除包含缺失值的记录。但是,行删除法是否合理,需要满足一个前提假定,即数据是完全随机缺失(MCAR),若不满足此条件,那么删除行会产生有偏的结果。
数据填补:根据研究设计不同,填补的方法有多种,如对于重复观察结果采用的末次观测结转(LOCF:Last observation carried forward),以及平时常用的简单插补法(即用某个值(如均值、中位数或众数)来替换变量中的缺失值)。这里只介绍在面对复杂的缺失值问题时,常用的多重插补法(MI,Multiple imputation),此处使用前面提到的R语言的mise包,其他软件也有类似的函数或者包。
3.4.3.2 末次观测结转(MI,Multiple imputation)
末次观测结转常被用于长期随访研究或者纵向研究中的缺失值填补,如临床试验或者队列研究中。其原理十分简单:将缺失值替换为其之前最近的非缺失值。通过自编函数的方式也可以很容易实现,在R已有较多的第三方包提供了对应的函数,如zoo包中的na.locf()函数以及DescTools包中的LOCF()函数。假设有如表3-8所示研究数据,用于记录每个老年人每季度的血糖值,但某个季度的血糖值缺失时,则可以考虑使用末次观测结转法进行填补,具体代码如下,填补后结果如表3-8最右列所示。在使用末次观测结转法时,有三点需要注意:1)对于首次观测结果为缺失时不使用;2)末次观测结转一定是与分组运算相结合的;3)填补前一定要将个体和时间变量进行升序排序。
#---数据集---#
df <-
expand.grid("id" = c("P01", "P02"),
"season" = c("S1", "S2", "S3", "S4"))
df$glu <- c(11.2, 7.8, NA, NA, 12.3, NA, 13.1, 10.2)
#---LOCF---#
library(dplyr)
library(zoo)
library(DescTools)
df_locf <-
df %>% arrange(id, season) %>%
group_by(id) %>%
mutate(glu_fill1 = na.locf(glu),
glu_fill2 = LOCF(glu))
print(df_locf)# A tibble: 8 × 5
# Groups: id [2]
id season glu glu_fill1 glu_fill2
<fct> <fct> <dbl> <dbl> <dbl>
1 P01 S1 11.2 11.2 11.2
2 P01 S2 NA 11.2 11.2
3 P01 S3 12.3 12.3 12.3
4 P01 S4 13.1 13.1 13.1
5 P02 S1 7.8 7.8 7.8
6 P02 S2 NA 7.8 7.8
7 P02 S3 NA 7.8 7.8
8 P02 S4 10.2 10.2 10.23.4.3.3 多重插补法(MI,Multiple imputation)
原理:
MI是将从一个包含缺失值的数据集中生成一组完整的数据集(通常是3到10个)。每个模拟数据集中,缺失数据将用蒙特卡洛方法来填补。缺失值的插补通过Gibbs抽样完成。每个包含缺失值的变量都默认可通过数据集中的其他变量预测得来,于是这些预测方程便可用来预测缺失数据的有效值。该过程不断迭代直到所有的缺失值都收敛为止。对于每个变量,用户可以选择预测模型的形式(称为基本插补法)和待选入的变量。默认地,预测的均值用来替换连续型变量中的缺失数据,而Logistic或多元Logistic回归则分别用来替换二值目标变量(两水平因子)或多值变量(多于两水平的因子)。其他基本插补法包括贝叶斯线性回归、判别分析、两水平正态插补和从观测值中随机抽样。用户也可以选择自己独有的方法。
语法:
函数mice()首先从一个包含缺失数据的数据框开始,然后返回一个包含多个(默认为5个)完整数据集的对象。每个完整数据集都是通过对原始数据框中的缺失数据进行插补而生成的。由于插补有随机的成分,因此每个完整数据集都略有不同。然后,with()函数可依次对每个完整数据集应用统计模型(如线性模型或广义线性模型),最后,pool()函数将这些单独的分析结果整合为一组结果。
- m为生成的数据集个数,默认为5个, seed是设定种子数,保证填补结果的可重复性,值可任意设定。
- 导出需要的填补完整数据集,action表示选择哪一个。
library(mice)
imp <- mice(df, m,
seed = 1234, method = "pmm")
sleep_im <- complete(pooled, action = 3) method为默认插补方式,pmm为默认方式预测均值匹配(Predictive mean matching), 还有一些其他methods插补方法:
- 贝叶斯线性回归(norm)。
- 基于bootstrap的线性回归(norm.boot)。
- 线性回归预测值(norm.predict)。
- 分类回归树(cart)。
- 随机森林(rf)。
使用这些插补方法对数据有严格的要求,比如贝叶斯线性回归等前三个模型都需要数据符合numeric格式,而pmm、cart、rf任意格式都行。
使用以上模型遇见的问题有:
pmm相当于某一指标的平均值作为插补,会出现插补值重复的问题。
cart以及rf是挑选某指标中最大分类的那个数字,是指标中的某一个数字,未按照规律。
要使用norm.predict,必须先对数据进行格式转换,这个过程中会出现一些错误。
实例:
library(mice)
imp <- mice(sleep, seed = 1234, method = "pmm")
iter imp variable
1 1 NonD Dream Sleep Span Gest
1 2 NonD Dream Sleep Span Gest
1 3 NonD Dream Sleep Span Gest
1 4 NonD Dream Sleep Span Gest
1 5 NonD Dream Sleep Span Gest
2 1 NonD Dream Sleep Span Gest
2 2 NonD Dream Sleep Span Gest
2 3 NonD Dream Sleep Span Gest
2 4 NonD Dream Sleep Span Gest
2 5 NonD Dream Sleep Span Gest
3 1 NonD Dream Sleep Span Gest
3 2 NonD Dream Sleep Span Gest
3 3 NonD Dream Sleep Span Gest
3 4 NonD Dream Sleep Span Gest
3 5 NonD Dream Sleep Span Gest
4 1 NonD Dream Sleep Span Gest
4 2 NonD Dream Sleep Span Gest
4 3 NonD Dream Sleep Span Gest
4 4 NonD Dream Sleep Span Gest
4 5 NonD Dream Sleep Span Gest
5 1 NonD Dream Sleep Span Gest
5 2 NonD Dream Sleep Span Gest
5 3 NonD Dream Sleep Span Gest
5 4 NonD Dream Sleep Span Gest
5 5 NonD Dream Sleep Span Gestsleep_im <- complete(imp, action = 1)
#查看填补情况
imp$imp$Dream 1 2 3 4 5
1 0.0 0.5 0.5 0.5 0.3
3 0.5 1.4 1.5 1.5 1.3
4 3.6 4.1 3.1 4.1 2.7
14 0.3 1.0 0.5 0.0 0.0
24 3.6 0.8 1.4 1.4 0.9
26 2.4 0.5 3.9 3.4 1.2
30 2.6 0.8 2.4 2.2 3.1
31 0.6 1.3 1.2 1.8 2.1
47 1.3 1.8 1.8 1.8 3.9
53 0.5 0.5 0.6 0.5 0.3
55 2.6 3.6 2.4 1.8 0.5
62 1.5 3.4 3.9 3.4 2.2检查插补效果:
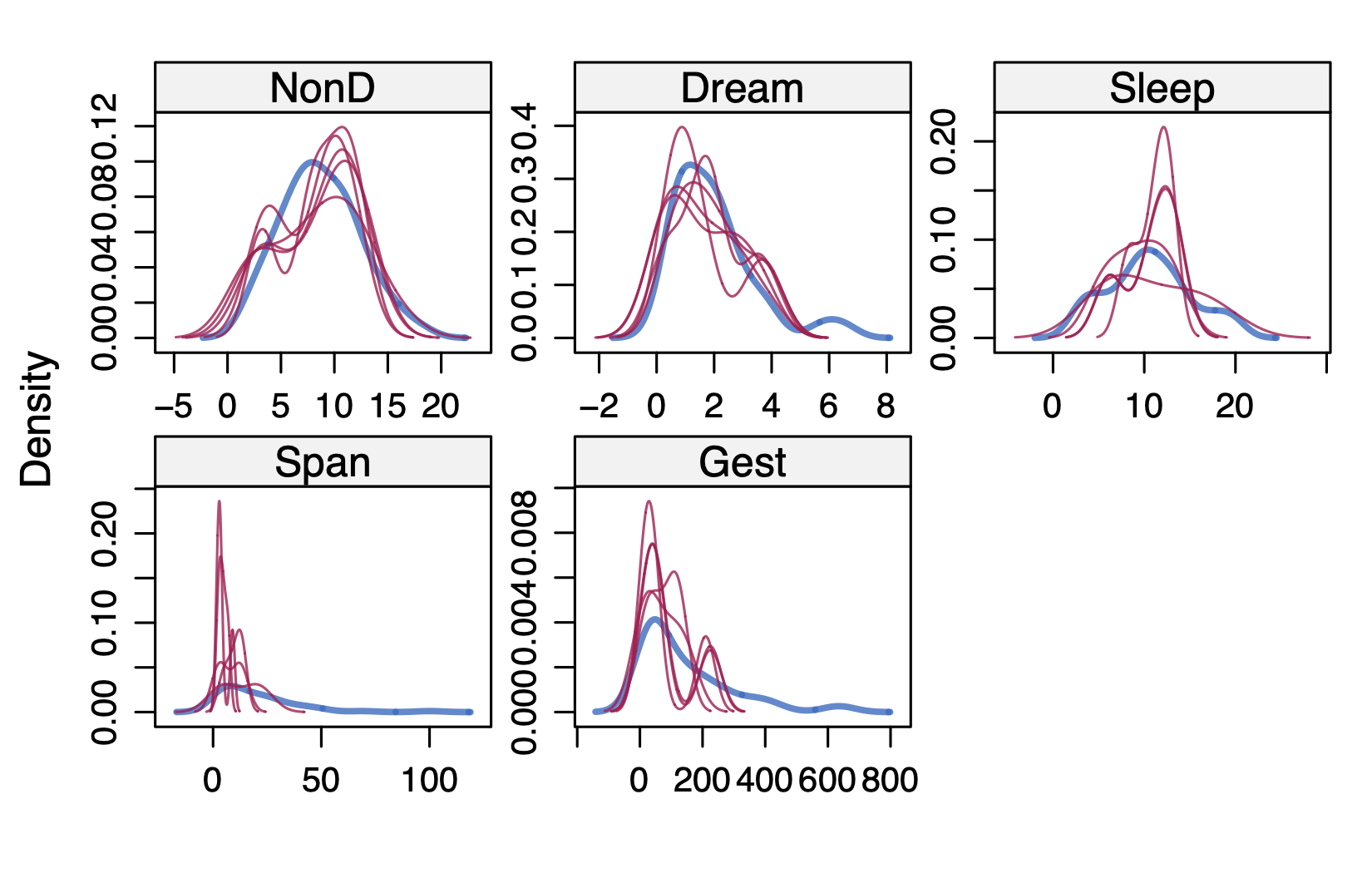
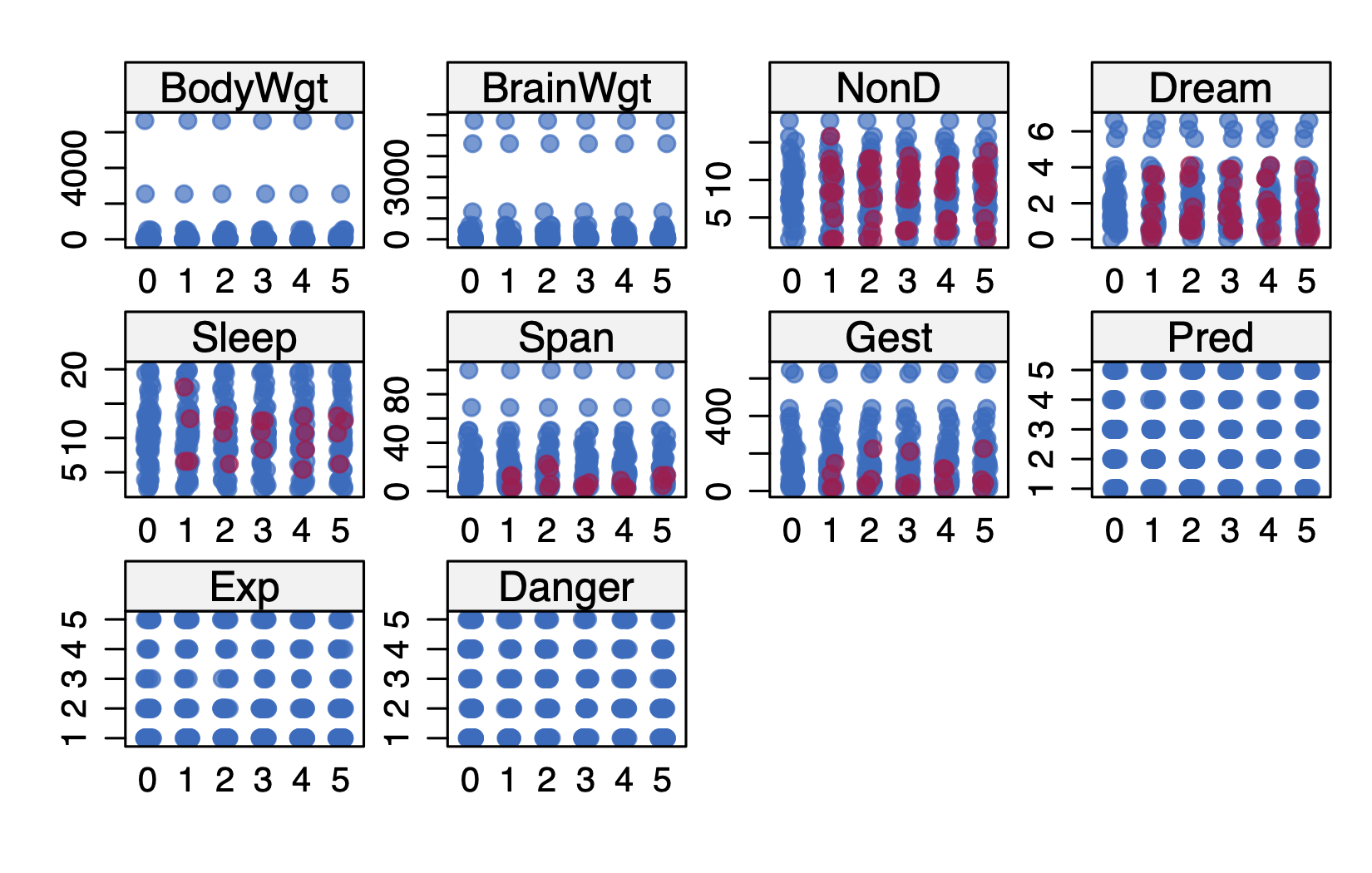
通过散点图和分布图,检查填补数据的效果,图 3.7 ,红色点表示填补值,蓝色表示非填补值。
library(lattice)
xyplot(imp, Dream ~ Gest + Span,
pch = 18, cex = 1)
densityplot(imp)
stripplot(imp, pch = 20, cex = 1.2)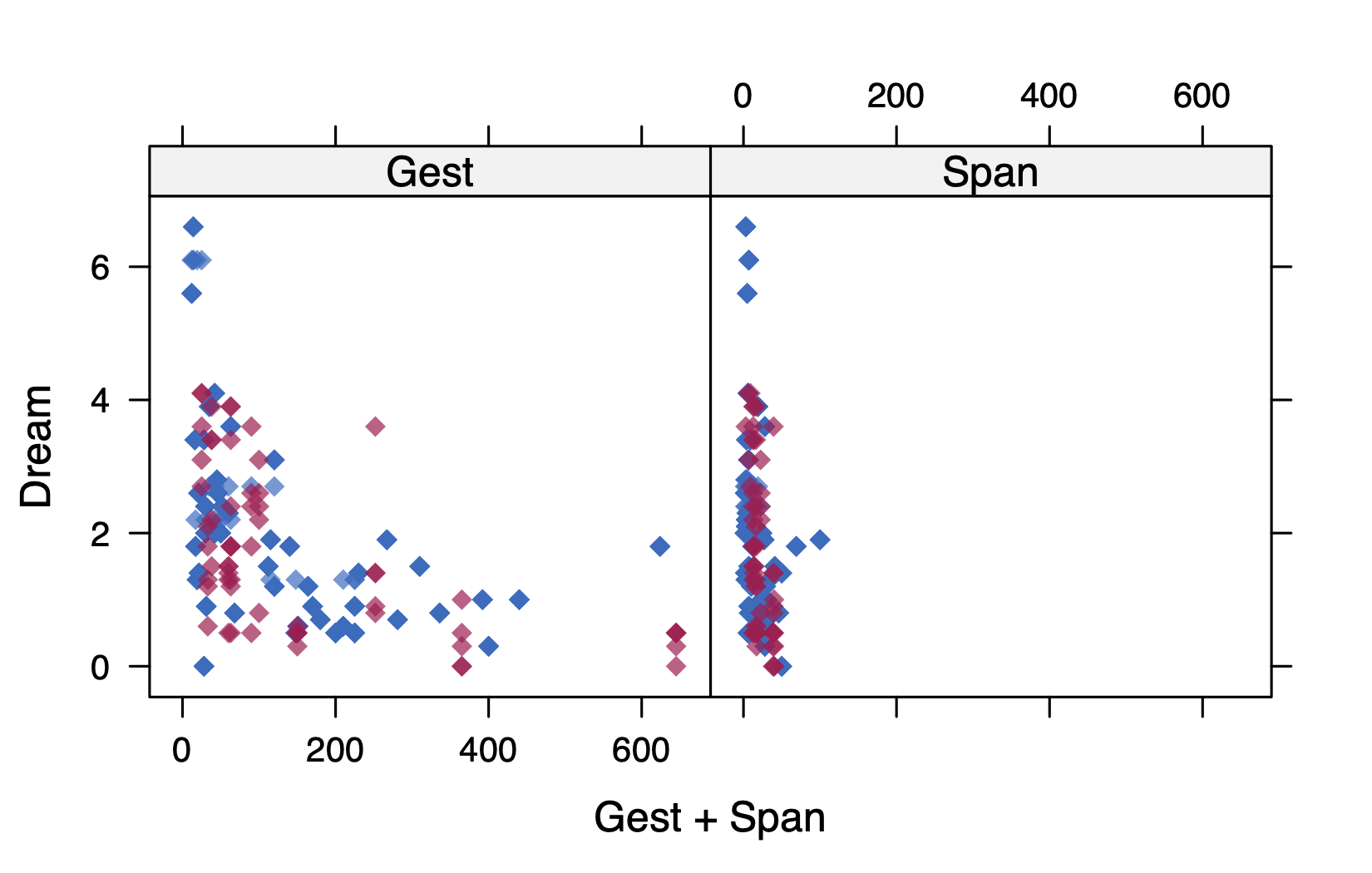
填补后数据集应用:
通常情况下,填补完成后,通常会进行回归分析,如前所示,MI填补生成了5个填补数据集,此时就会有一个疑问,到底选择哪一个作为最后的完整数据集。mice包提供了一个函数可以很容易的将5个填补数据集分别进行回归,然后将结果合并后返回一个结果。
sleep_im_fit <- with(imp,
lm(Sleep ~ Gest + Span))
modelsummary::modelsummary(sleep_im_fit,
stars = TRUE,
output = "gt")| (1) | |
|---|---|
| (Intercept) | 13.174*** |
| (0.732) | |
| Gest | -0.016*** |
| (0.005) | |
| Span | -0.020 |
| (0.035) | |
| + p < 0.1, * p < 0.05, ** p < 0.01, *** p < 0.001 | |
处理一般线性回归的lm()函数,其他方法包括广义线性模型glm()函数、广义可加模型gam(),负二项模型nbrm()函数均可实现。
本书中所讲的数值型变量是指根据统计学中的标准划分的计量和计数指标,而非指数据库中存储为Int或者Float类型的变量。↩︎