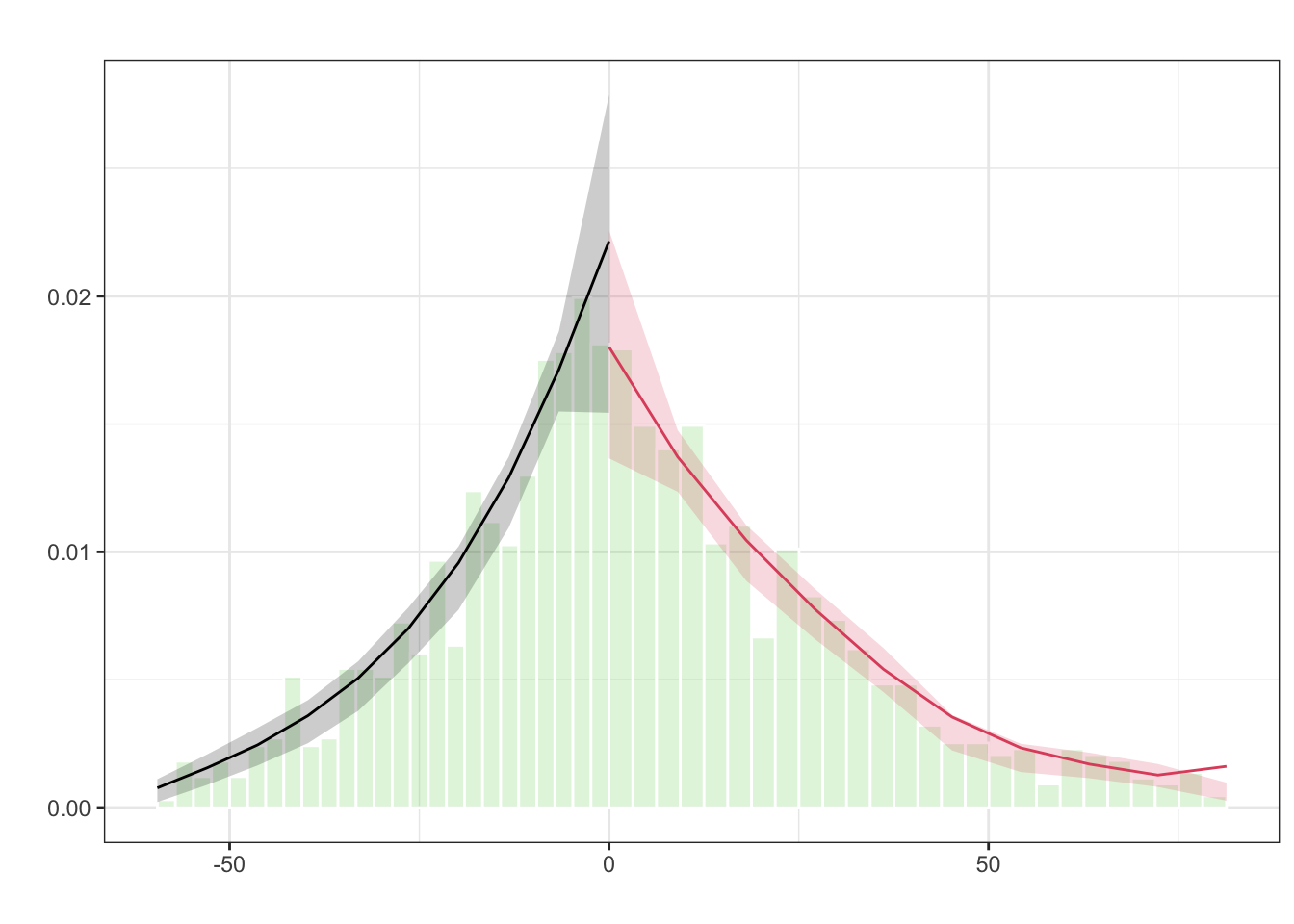
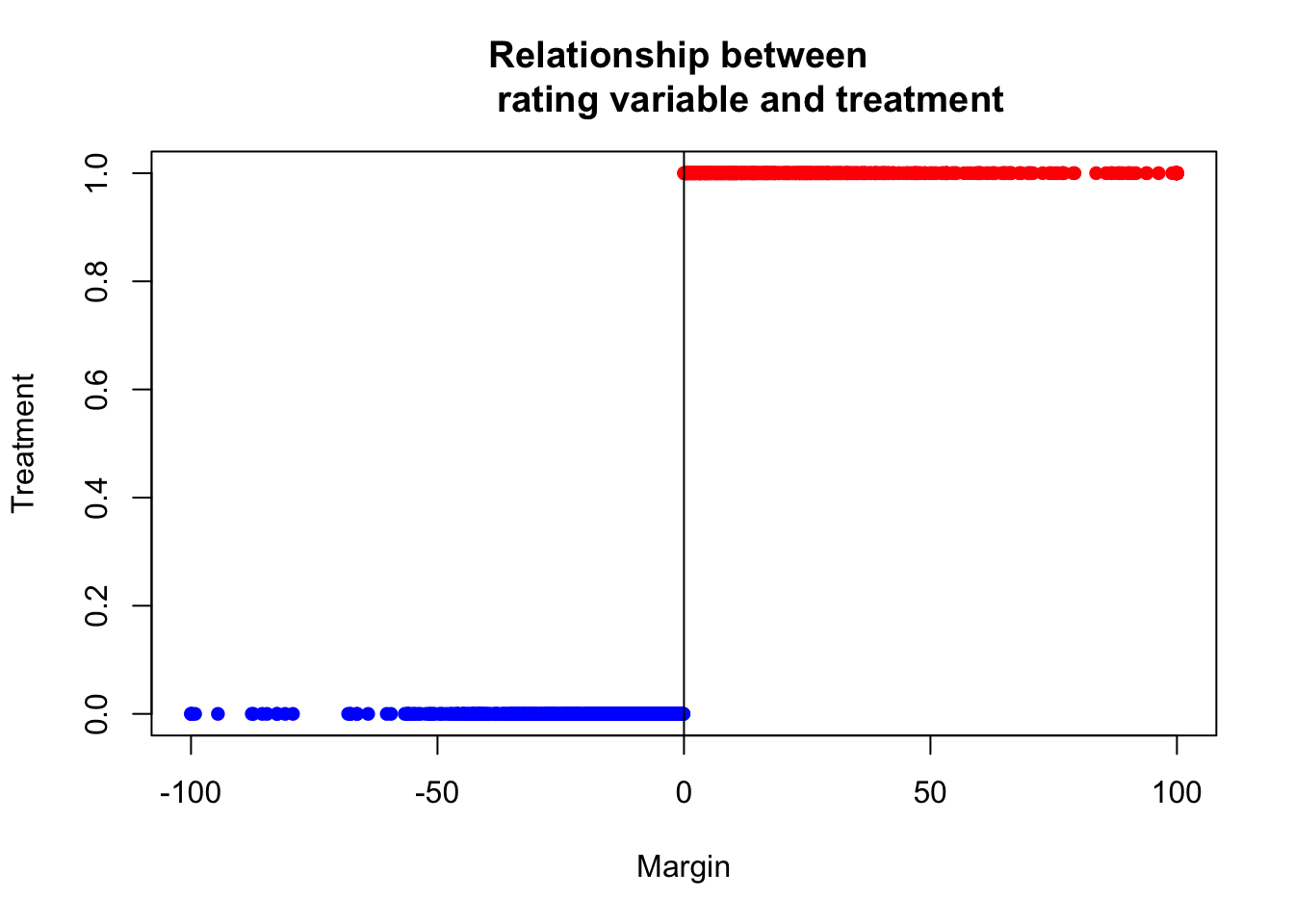
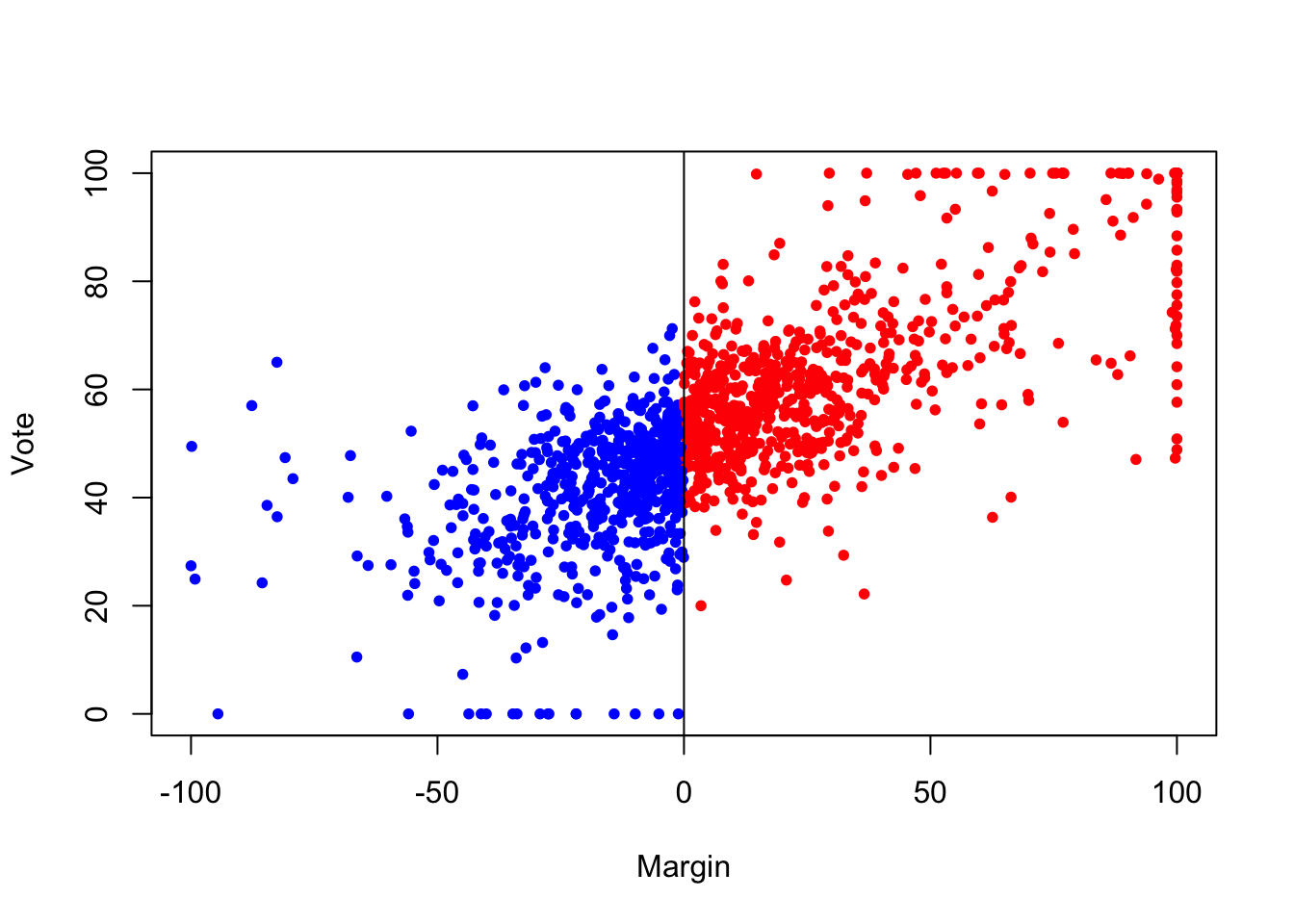
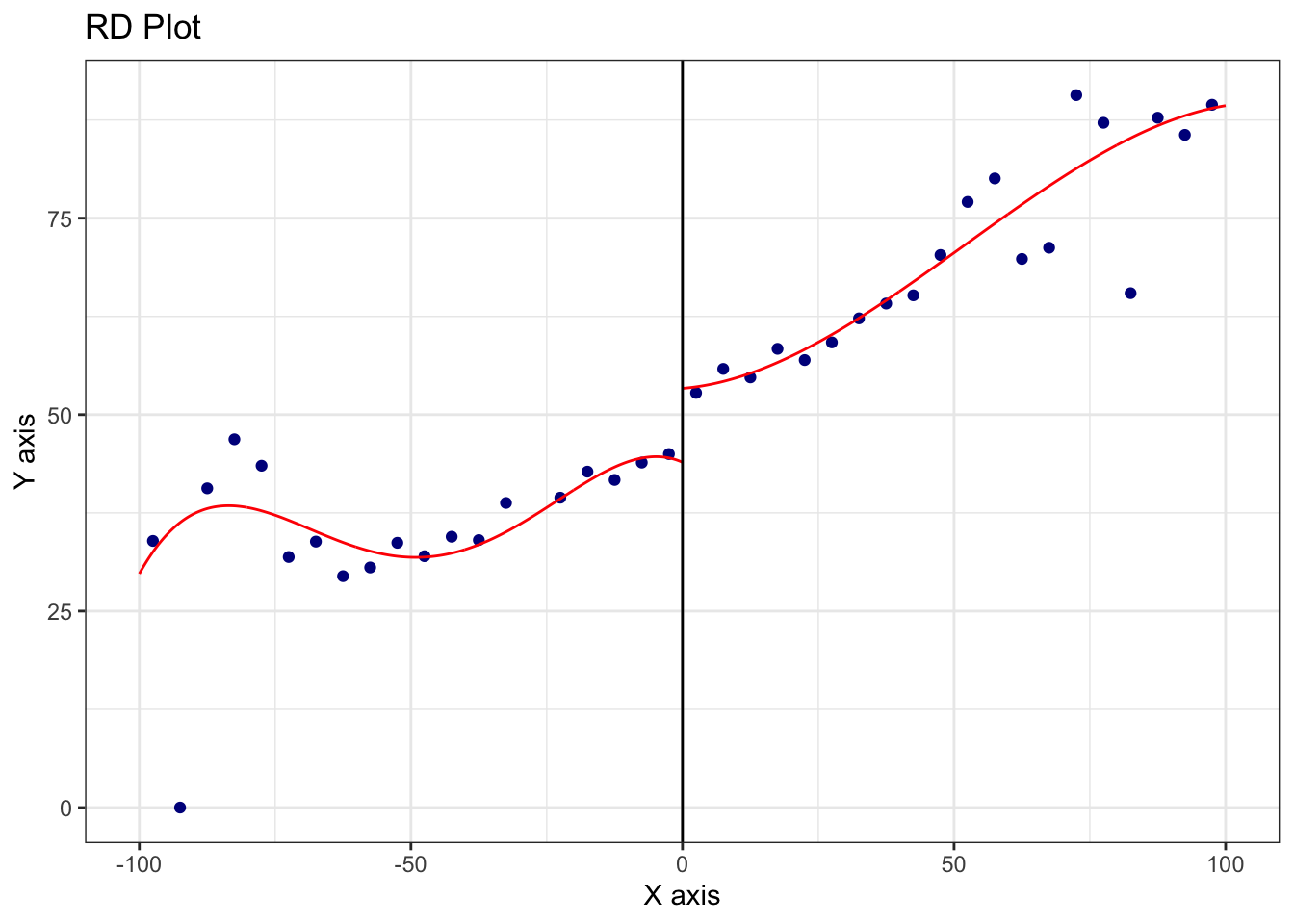
由于真实世界的复杂性,对因果推断的分析方法的要求也越来越高,没有一种方法可以适用所有的情形,因此RD的方法也衍生发展出很多类型,包括多个断点(Multi-Cutoff RD Design)、多个驱动变量(Multi-Score RD Design)、离散驱动变量(Multi-Score RD Design)等等。
Angrist J D. Pischke J S. 2009. Mostly Harmless Econometrics: An Empiricist’s Companion[M]. Princeton, New Jersey Oxford: Princeton University Press.
Ashenfelter O. Card D. 1985. Using the
Longitudinal Structure of
Earnings to
Estimate the
Effect of
Training Programs[J/OL]. The Review of Economics and Statistics, 67(4): 648.
https://www.jstor.org/stable/1924810.
Blackwell M. Iacus S. King G. 等. 2009. Cem:
Coarsened Exact Matching in
Stata[J/OL]. The Stata Journal: Promoting Communications on Statistics and Stata, 9(4): 524-546[2025-05-31].
https://doi.org/10.1177/1536867X0900900402.
Böckerman P. Ilmakunnas P. 2009. Unemployment and Self-assessed Health: Evidence from Panel Data[J/OL]. Health Economics, 18(2): 161-179[2025-04-12].
https://doi.org/10.1002/hec.1361.
Callaway B. Sant’Anna P H C. 2021. Difference-in-
Differences with Multiple Time Periods[J/OL]. Journal of Econometrics, 225(2): 200-230[2021-12-07].
https://doi.org/10.1016/j.jeconom.2020.12.001.
Calonico S. Cattaneo M D. Farrell M H. 等. 2022. rdrobust: Robust Data-Driven Statistical Inference in Regression-Discontinuity Designs[M/OL].
https://CRAN.R-project.org/package=rdrobust.
Cochran A W G. 1968. The Effectiveness of Adjustment by Subclassification in Removing Bias in Observational Studies Published by : International Biometric Society Linked references are available on JSTOR for this article : THE EFFECTIVENESS OF ADJUSTMVIENT BY[J].
Cunningham S. 2021. Causal Inference: The Mixtape[M]. New Haven ; London: Yale University Press.
D. Cattaneo M. Idroboy N. Titiunik R. 2017. A Practical Introduction to Regression Discontinuity Designs: Volume I[M]. collingwoodresearch.com.
Daw J R. Hatfield L A. 2018. Matching and
Regression to the
Mean in
Difference-in-
Differences Analysis[J/OL]. Health Services Research, 53(6): 4138-4156[2025-04-12].
https://doi.org/10.1111/1475-6773.12993.
Dimick J B. Ryan A M. 2014. Methods for
Evaluating Changes in
Health Care Policy:
The Difference-in-Differences Approach[J/OL]. JAMA, 312(22): 2401[2025-04-12].
https://doi.org/10.1001/jama.2014.16153.
Goodman-Bacon A. 2021. Difference-in-Differences with Variation in Treatment Timing[J/OL]. Journal of Econometrics, 225(2): 254-277[2025-04-15].
https://doi.org/10.1016/j.jeconom.2021.03.014.
Iacus S M. King G. Porro G. 2009.
Cem :
Software for
Coarsened Exact Matching[J/OL]. Journal of Statistical Software, 30(9)[2025-05-31].
https://doi.org/10.18637/jss.v030.i09.
Iacus S M. King G. Porro G. 2011. Multivariate
Matching Methods That Are Monotonic Imbalance Bounding[J/OL]. Journal of the American Statistical Association, 106(493): 345-361[2025-05-31].
https://doi.org/10.1198/jasa.2011.tm09599.
Iacus S M. King G. Porro G. 2012. Causal
Inference without
Balance Checking:
Coarsened Exact Matching[J/OL]. Political Analysis, 20(1): 1-24[2025-05-31].
https://doi.org/10.1093/pan/mpr013.
Jacob R. Zhu P. Marie-Andrée. 2012. A Practical Guide to Regression Discontinuity[M]. MDRC.org.
Kahn-Lang A. Lang K. 2020. The
Promise and
Pitfalls of
Differences-in-Differences:
Reflections on
16 and Pregnant and
Other Applications[J/OL]. Journal of Business & Economic Statistics, 38(3): 613-620[2025-04-11].
https://doi.org/10.1080/07350015.2018.1546591.
Lalonde R. 1984. Evaluating the Econometric Evaluations of Training Programs with Experimental Data[J]. The American Economic Review, 76.
Rosenbaum P R. Rubin D B. 1983. The Central Role of the Propensity Score in Observational Studies for Causal Effects[J/OL]. Biometrika, 70(1): 41-55[2025-04-14].
https://doi.org/10.1093/biomet/70.1.41.
Rubin D B. 1980. andomization Analysis of Experimental Data in the Fisher Randomization Test[J/OL]. Journal American Statistical Association, 75(371).
https://www.jstor.org/stable/.
Ryan A M. Burgess J F. Dimick J B. 2015. Why
We Should Not Be Indifferent to
Specification Choices for
Difference-in-
Differences[J/OL]. Health Services Research, 50(4): 1211-1235[2025-04-12].
https://doi.org/10.1111/1475-6773.12270.
Soumerai S B. Koppel R. 2017. The
Reliability of
Instrumental Variables in
Health Care Effectiveness Research:
Less Is More[J/OL]. Health Services Research, 52(1): 9-15[2025-07-04].
https://doi.org/10.1111/1475-6773.12527.
Stuart E A. 2010. Matching
Methods for
Causal Inference:
A Review and a
Look Forward[J/OL]. Statistical Science, 25(1)[2025-05-30].
https://doi.org/10.1214/09-STS313.
Stuart E A. Huskamp H A. Duckworth K. 等. 2014. Using Propensity Scores in Difference-in-Differences Models to Estimate the Effects of a Policy Change[J/OL]. Health Services and Outcomes Research Methodology, 14(4): 166-182[2025-04-12].
https://doi.org/10.1007/s10742-014-0123-z.
Sun L. Abraham S. 2021. Estimating Dynamic Treatment Effects in Event Studies with Heterogeneous Treatment Effects[J/OL]. Journal of Econometrics, 225(2): 175-199[2025-04-15].
https://doi.org/10.1016/j.jeconom.2020.09.006.
Walker V. Sanderson E. Levin M G. 等. 2024. Reading and Conducting Instrumental Variable Studies: Guide, Glossary, and Checklist[J/OL]. BMJ: e078093[2025-07-04].
https://doi.org/10.1136/bmj-2023-078093.
Wooldridge J M. 2009. Introductory econometrics: a modern approach[M]. 4. ed. Peking: Cengage Learning.
刘冲. 沙学康. 张妍. 2022. 交错双重差分:处理效应异质性与估计方法选择[J/OL]. 数量经济技术经济研究, 39(09): 177-204.
https://doi.org/10.13653/j.cnki.jqte.20220805.001.
许文立. 2023. 双重差分法的最新理论进展与经验研究新趋势[J]. 广东社会科学(05): 51-62.
谢谦. 薛仙玲. 付明卫. 2019. 断点回归设计方法应用的研究综述[J]. 经济与管理评论, 35(2): 11.
黄丽红. 陈峰. 2019. 倾向性评分方法及其应用[J]. 中华预防医学杂志, 53(7): 5.
黄炜. 张子尧. 刘安然. 2022. 从双重差分法到事件研究法[J/OL]. 产业经济评论(02): 17-36.
https://doi.org/10.19313/j.cnki.cn10-1223/f.20211227.002.